Che cos’è un triangolo rettangolo isoscele e di quali proprietà gode? Esistono delle formule particolari per calcolare perimetro ed area? In questa lezione troverai spiegato in maniera semplice tutto ciò che riguarda il triangolo isoscele rettangolo.
Che cos’è
Il triangolo rettangolo isoscele è un triangolo che ha due lati uguali e un angolo di 90°.
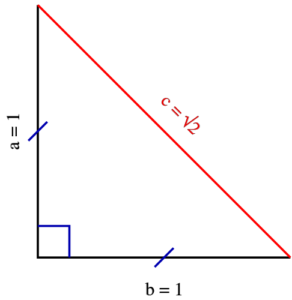
Analizzando la definizione appena esposta e la figura al lato possiamo fare una serie di considerazioni molto utili che ci aiuteranno a trovare delle formule semplici da ricordare e soprattutto da ricavare.
Approfondimenti: tutte le proprietà del triangolo isoscele
La prima osservazione oggettiva da fare sul triangolo rettangolo isoscele è che l’angolo retto è compreso tra i due lati uguali. Quindi questo significa che i due cateti sono uguali.
Hai notato inoltre che il triangolo rettangolo isoscele è metà quadrato? L’ipotenusa del triangolo non è altro che la diagonale del quadrato.
Dato infatti il triangolo rettangolo in figura, chiamiamo a, b, e c i tre lati. Nell’immagine laterale trovi che i due cateti sono pari ad uno, ma si tratta solo di un esempio per dimostrarti che essi sono congruenti, cioè uguali. Chiamiamo il perimetro p e l’area A.
Formule
In questa figura geometrica si vanno a riprendere le formule del triangolo isoscele con alcune ulteriori semplificazioni dovute al fatto che c’è un angolo di 90°.
- a=b=cateti → la relazione esprime l’uguaglianza tra i due cateti
- Perimetro triangolo rettangolo iscoscele a+b+c=p → 2a+c=p
- Ampiezza degli angoli: 45°, 45°, 90°.
- Area triangolo rettangolo isoscele (a⋅b)/2=A →a2/2=A
- Teorema di Pitagora: a2+b2=c2 → 2a2=c2 →a√2=c
Quest’ultima relazione ci mostra come a partire da un cateto si possa calcolare l’ipotenusa semplicemente calcolando per radice di due. Valgono ovviamente tutte le formule inverse. Quindi si potrà calcolare il cateto conoscendo il perimetro, oppure l’area, oppure l’ipotenusa. Allo stesso modo possiamo dire che si potrà calcolare l’ipotenusa partendo dal perimetro, dall’area o dal cateto.
Consiglio
Generalmente non è necessario ricordare le formule viste sopra, né gli insegnanti le richiedono. Tuttavia è fondamentale ricordare quali sono le caratteristiche di questa figura particolare. In questo modo potrai ricavare e usare le formule del triangolo rettangolo isoscele senza impararle a memoria. Tu devi solo ricordarti che, essendo un triangolo isoscele rettangolo ha due lati uguali, due angoli uguali e un angolo retto.
Proprietà
Vediamo di approfondire in maniera più dettagliata quelle che sono le proprietà del triangolo rettangolo isoscele.
Gli angoli adiacenti all’ipotenusa misurano 45°
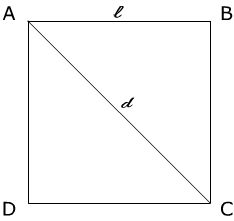
Abbiamo infatti detto che il triangolo isoscele rettangolo è la metà di un quadrato. Te ne puoi accorgere dalla figura sulla destra. La diagonale del quadrato è anche bisettrice dell’angolo DAB e BCD. Questo vuol dire che gli angoli DAC e ACD sono di 45°.
L’altezza relativa all’ipotenusa è anche mediana e bisettrice
Questo perché i due cateti sono uguali. Questo vuol dire che tracciando da D l’altezza sul segmento AC, quest’ultimo resta diviso in due parti e lo stesso si può dire per l’angolo in D. Si nota che l’altezza relativa all’ipotenusa DH (prova a disegnarla su un foglio) diventa asse di simmetria del triangolo ADC.
L’area del triangolo isoscele rettangolo è metà di quella del quadrato
Abbiamo già ripetuto che questo triangolo particolare è metà quadrato. Questo significa che possiamo ricavarci la sua area anche in maniera differente. Si calcola infatti l’area del quadrato l2=A e la si divide per due per ottenere anche l’area del triangolo.
Esercizi sul triangolo rettangolo isoscele
L’area del triangolo isoscele rettangolo misura 144 m2. Calcolare il perimetro.
Svolgimento
Abbiamo detto che possiamo usare una formula diversa dalla classica dei triangoli (bxh/2=A). In questo caso si può scrivere cateto2/2=A. Applicando la formula inversa possiamo quindi calcolare quanto vale il cateto (che chiamiamo c per semplicità):
c2=2A → √c2=√(2A) → c=√(2A)
Per ottenere la formula inversa abbiamo portato prima moltiplicato ambo i membri per 2, poi fatto la radice quadrata di tutto. In questo modo abbiamo ottenuto la formula del cateto a partire dall’area del triangolo rettangolo isoscele.
Andiamo ora a sostituire i dati:
c=√(2⋅144)=12√2
Una volta calcolato il cateto, si può calcolare l’ipotenusa (che indicheremo con i) con il teorema di Pitagora.
c√2=i → i=12√2(√2)
i=12⋅2=24
Avendo anche l’ipotenusa, a questo punto possiamo calcolare il perimetro del triangolo rettangolo isoscele:
p=2c+i=2⋅12√2+24 = 24√2+24
In base a quanto abbiamo detto anche nella lezione sulla somma di radicali, queste due radici non sono simili per cui non si possono sommare. Per questa ragione non si possono eseguire altri passaggi e l’esercizio può considerarsi concluso. Ti starai chiedendo: si, ma quel numero quanto vale?? Se provi a scriverlo sulla calcolatrice ti uscirà che il perimetro è circa pari a p=57,94 cm.
molto grato per la semplicità dell esposizione .