Il triangolo isoscele è un triangolo con la proprietà di avere 2 lati uguali e di conseguenza anche due angoli uguali.
In questa lezione tratteremo tutto quello che riguarda il triangolo isoscele, dandoti tutti i link di approfondimento alle lezioni sulle formule da usare o sui vari elementi geometrici caratteristici. Iniziamo subito vedendo che cos’è questo poligono elementare e come si disegna.
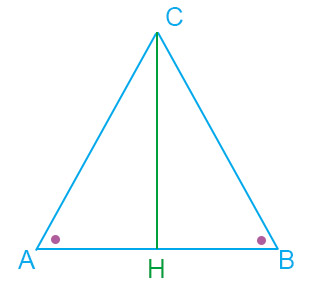
Dal disegno in figura si definiscono:
AB = base;
AC = CB sono i due lati congruenti;
CAB = ABC sono i due angoli congruenti;
CH = altezza relativa alla base AB.
Quindi la sostanziale differenza, rispetto ad un triangolo scaleno, è che in questo caso abbiamo due lati e due angoli tra loro congruenti.
Formule triangolo isoscele
Quali sono le formule da utilizzare nei problemi che riguardano questa figura geometrica? Nella lezione sulle formule del triangolo isoscele trovi il formulario completo con tutte le formule inverse e gli esercizi svolti.
Ecco elencate le principali:
| Perimetro del triangolo isoscele | 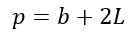 |
| Area del triangolo isoscele | 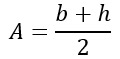 |
| Lato obliquo con Pitagora | 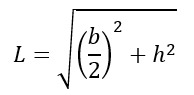 |
Approfondimenti: area del triangolo isoscele
Da notare che compare la formula del teorema di Pitagora. Poiché infatti l’altezza divide la figura in due triangoli rettangoli, molto spesso si scompone il problema e dal triangolo isoscele si passa a quello rettangolo.
Proprietà del triangolo isoscele
Riassumiamo di seguito quelle che sono le caratteristiche principali di questo poligono:
- lati obliqui e angoli alla base sono congruenti;
- è simmetrico rispetto all’altezza relativa alla base (vedi la lezione sulla simmetria assiale);
- l’altezza relativa alla base divide la figura in due triangoli rettangoli uguali;
- il triangolo equilatero è un particolare tipo di triangolo isoscele con la base uguale ai lati obliqui;
- l’altezza relativa alla base è anche mediana, asse e bisettrice dell’angolo al vertice;
- può essere acutangolo o ottusangolo.
- in un triangolo isoscele inscritto in una circonferenza la distanza dal centro della circonferenza dai vertici del triangolo è costante.
Approfondimenti: triangolo equilatero inscritto in una circonferenza
Triangoli isosceli particolari
- Il triangolo da 30-60-90 è un triangolo rettangolo isoscele che ha, oltre all’angolo retto, gli altri due angoli che misurano 30° e 60°. La particolarità è che la base pari alla metà della misura dell’ipotenusa.
- Il triangolo da 45-45-90 è un triangolo rettangolo isoscele che si ottiene suddividendo a metà un quadrato. La proprietà di questa figura è che i due cateti sono congruenti.
Come calcolare la misura degli angoli?
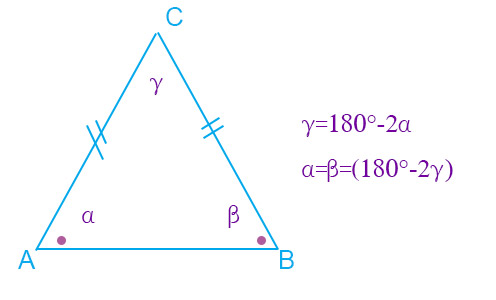
Una delle domande più frequenti che ci pongono gli studenti riguarda il calcolo degli angoli del triangolo isoscele. Il procedimento risolutivo è molto semplice. Ricorda che la somma degli angoli interni di un triangolo è pari a 180° (cioè sono angoli supplementari), per cui basta avere nota la misura di uno degli angoli per poter calcolare la differenza:
Conclusioni
In questa prima lezione abbiamo visto una rapida sintesi su tutto quello che c’è da sapere sui triangoli isosceli. Trovi tutte le informazioni aggiuntive di cui hai bisogno all’interno dei vari link che hai incontrato durante la lettura. Se c’è qualche argomento che non abbiamo ancora trattato o hai un dubbio che non riesci a risolvere, o se anche semplicemente questa lezione ti è stata utile, lasciaci un tuo feedback nei commenti in basso! Buono studio!