Triangolo di Tartaglia spiegazione ed esempi

Il triangolo di Tartaglia è una tabella contenente un insieme di numeri utili per risolvere l’elevazione a potenza di un qualsiasi binomio del tipo:

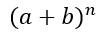
Molti nostri studenti ci chiedono, dopo aver studiato il cubo di un binomio, come si risolve un binomio alla quarta. Il triangolo di Tartaglia è proprio lo strumento più veloce per svolgere un esercizio di questo tipo.

A che serve il triangolo di Tartaglia?

Grazie a questa tabella, è possibile determinare quelli che vengono chiamati coefficienti binomiali. Non ne hai mai sentito parlare? Non preoccuparti: ricordi come si sviluppa un quadrato di binomio?

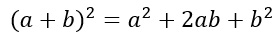
Proviamo a verificare quali sono i coefficienti che vengono fuori dal calcolo:

1 2 1

Attraverso il triangolo di Tartaglia riusciamo ad individuare i coefficienti qualsiasi sia l’esponente per cui è elevato un binomio.

Come si fa il triangolo di Tartaglia?

La prima considerazione che facciamo è che qualsiasi numero elevato a 0 mi dà come risultato 1. Per approfondimenti puoi andare a rileggerti la nostra lezione sulle proprietà delle potenze.

Il triangolo di Tartaglia si costruisce iniziando scrivendo proprio il numero 1, che corrisponde all’elevazione a potenza del binomio alla zero.

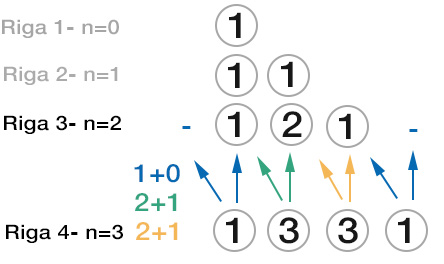
Sulla seconda riga della tabella mettiamo invece 2 numeri: ciascuno di questi è pari alla somma dei numeri della riga precedente che si trovano immediatamente sopra e a sinistra.

Da notare che il termine della freccia sinistra non sia presente, per cui la somma da effettuare è 1+0. Sulla seconda riga abbiamo un secondo termine sempre pari alla somma dei numeri sulla riga precedente che si trovano in alto e a sinistra.

Possiamo così passare alla riga successiva, corrispondente a n=3, ripetendo gli stessi calcoli.

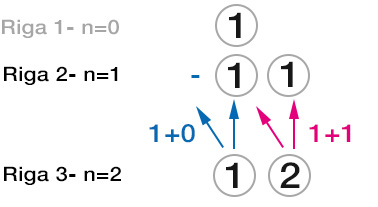
Mentre il primo sarà sempre uguale a 1, il secondo questa volta è pari a 1+1, cioè 2. L’ultimo termine invece è sempre 1.

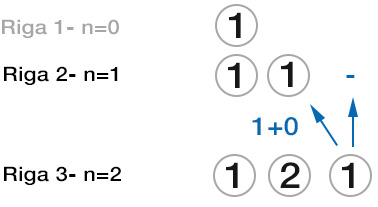
Passiamo così alla riga 4, corrispondente a n=3.

Si può continuare in questo modo praticamente all’infinito per avere qualsiasi esponente n di cui si abbia necessità. Per cui possiamo scrivere il triangolo di Tartaglia come nella tabella che segue:

Come calcolare le potenze di un binomio

Immaginiamo di voler calcolare ad esempio la potenza 4 del binomio a+b. Quindi l’esponente è n=4. Per semplicità ti evidenzio la riga corrispondente sulla tabella.

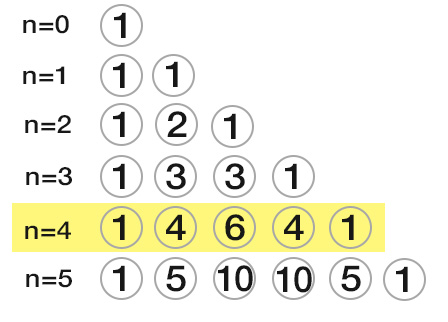
Attraverso il triangolo di Tartaglia so immediatamente che i coefficienti del binomio da elevare alla quarta saranno:

1 4 6 4 1

Ho quindi cinque elementi da individuare:

• il primo: si ottiene moltiplicando il primo coefficiente (1), per il primo monomio (a) elevato alla n, per il secondo monomio elevato a 0. Ricordando che qualsiasi potenza che abbia come esponente 0, mi dà come risultato 1, allora possiamo scrivere:

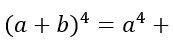
• il secondo: si ottiene allo stesso modo. Ricordati da ora che l’esponente del primo monomio (a) dovrà diminuire di 1, mentre l’esponente del secondo termine (b) dovrà aumentare di 1. Quindi otteniamo

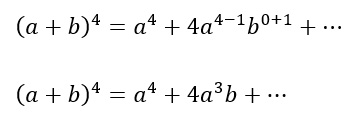
• e così via…: continuiamo a diminuire il primo esponente e ad aumentare il secondo, senza mai dimenticarci il coefficiente binomiale.

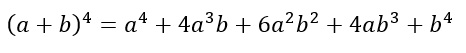
Triangolo di Tartaglia esercizi svolti

Una delle domande che potrebbe porsi lo studente è: ma come si applica il triangolo delle potenze quando compaiono delle potenze con il segno meno?? Vediamo subito in un esempio.

Risolvere l’espressione x meno 1 alla quinta.

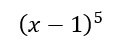
Torniamo sul triangolo di Tartaglia alla riga 6, corrispondente a n=5

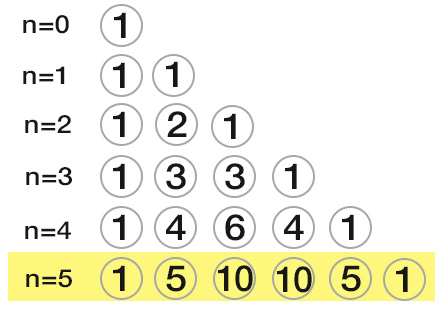
Abbiamo così 6 coefficienti da utilizzare:

1 – 5 – 10 – 10 – 5 – 1

Possiamo sviluppare quindi la potenza quinta utilizzando in maniera appropriata le parentesi tonde:

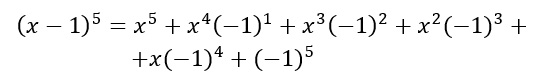
Grazie alle parentesi posso in questo modo risolvere passo passo senza paura di sbagliare i segni:

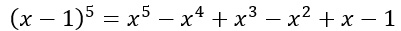
Esercizi da risolvere

Non resta che esercitarti con semplici tracce.

Da notare che l’ultimo esercizio include una radice quadrata. Se hai ben presente le regole delle radici, non spaventarti e prova a risolvere normalmente l’esercizio. Se segui alla lettera la regola che abbiamo studiato oggi assieme, vedrai che non avrai alcun problema.

CURIOSITA’ : Chi ha inventato il triangolo di Tartaglia? Il metodo era utilizzato già in tempi antichissimi dai cinesi, ma fu trattato in maniera più approfondita prima dal matematico Tartaglia nel XVI secolo e poi da Pascal nel XVII secolo.

Conclusioni

Se questa lezione ti è stata utile, lasciaci un commento. Un tuo feedback positivo ci è davvero utile per migliorare ogni giorno le nostre lezioni ed offrirti sempre più contenuti di qualità.