I teoremi della trigonometria sui triangoli rettangoli sono delle formule che mettono in relazione i cateti, l’ipotenusa e gli angoli del generico triangolo rettangolo. Nelle formule trigonometriche compaiono le funzioni goniometriche, cioè seno, coseno, tangente e cotangente.
I teoremi dei triangoli rettangoli in trigonometria sono utili per risolvere tantissimi tipi di problemi geometrici e potranno essere utilizzati anche in numerose applicazioni nel proseguo degli studi. Capita spesso anche nel problema dell’esame di stato di dover risolvere un triangolo rettangolo usando le formule trigonometriche.
Le formule trigonometriche sui triangoli rettangoli che vedremo in questa lezione vanno ad aggiungersi a quelle note della geometria euclidea e che hai già studiato alle scuole medie. Puoi trovare una tabella riepilogativa alla lezione sulle formule del triangolo rettangolo.
Di seguito indicheremo con A, B e C i vertici (disposti in genere in senso antiorario) di un triangolo qualsiasi, con α (alfa) β (beta) γ (gamma) le misure degli angoli di vertici rispettivamente A, B e C. Se il triangolo è rettangolo indicheremo con A il vertice dell’angolo retto e quindi con a la misura dell’ipotenusa, mentre b e c sono le misure dei due cateti e β e γ i due angoli acuti.
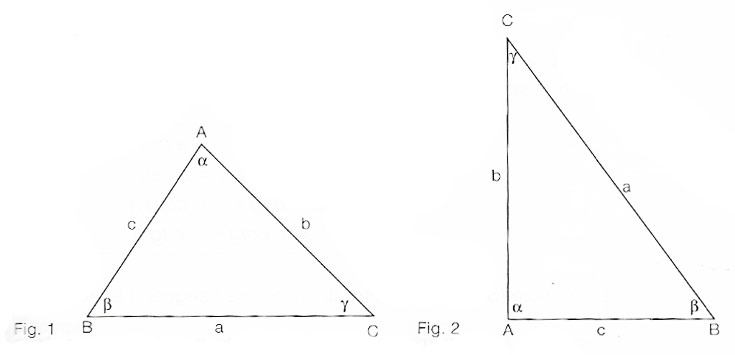
Primo teorema sui triangoli rettangoli
Enunciato: In un triangolo rettangolo la misura di un cateto è uguale a quella dell’ipotenusa moltiplicata per il seno dell’angolo opposto ad esso oppure per il coseno dell’angolo acuto ad esso adiacente.
AB = BC · senγ
AB = BC · cosβ
AC = BC · senβ
AC = BC · cosγ
Attraverso il primo teorema della trigonometria, in un triangolo rettangolo si può ottenere la misura del cateto conoscendo l’ipotenusa e il seno (o il coseno) dell’angolo opposto (o adiacente)
Formule Inverse
Sfruttando invece le formule inverse del primo teorema della trigonometria si possono trovare l’ipotenusa o gli angoli (ovviamente bisogna applicare l’arcoseno o l’arcocoseno). Per esempio dalla prima delle quattro formule viste, si possono ricavare:
- AB = BC · senγ → senγ = AB/BC → γ = arcsen(AB/BC)
- AB = BC · senγ → BC = AB/senγ
Dimostrazione I teorema trigonometria sui triangoli rettangoli
Partiamo dalla circonferenza goniometrica e dalla definizione di seno e coseno.
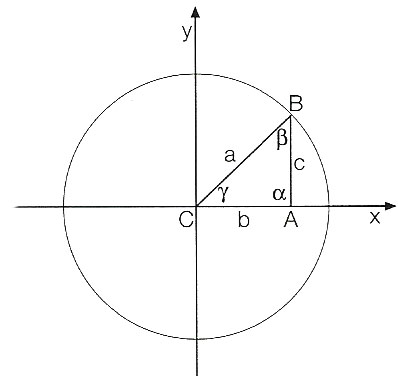
Per le definizioni viste avremo:
senγ=AB/BC
cosγ=AC/BC
Nel caso della circonferenza goniometrica, il raggio BC era pari a 1. Nel caso invece di un triangolo rettangolo generico, l’ipotenusa ha una misura generica. Con un semplice passaggio algebrico, alle due formule appena viste passiamo alle seguenti:
AB = senγ · BC
AC = cosγ · BC
L’angolo α=90°, mentre gli β e γ sono tra loro complementari. Questo significa che senβ=cosγ e senβ=senγ. Per cui possiamo scrivere le formule del primo teorema trigonometrico sul triangolo rettangolo:
AB = senγ · BC = cosβ · BC
AC = cosγ · BC = senβ · BC
Secondo teorema sui triangoli rettangoli
In un triangolo rettangolo la misura di un cateto è uguale a quella dell’altro cateto moltiplicata per la tangente dell’angolo opposto al primo cateto oppure per la cotangente dell’angolo acuto ad esso adiacente.
AB = AC · tgγ
AB = AC · cotgβ
AC = AB · tgβ
AC = AB · cotgγ
Attraverso il secondo teorema della trigonometria sul triangolo rettangolo, si può trovare un cateto avendo la misura dell’altro cateto e un angolo, opposto o adiacente non importa.
Formule inverse
Attraverso un semplice passaggio algebrico si possono ottenere le formule inverse che permettono sostanzialmente di trovare l’angolo conoscendo i due cateti. Bisogna ovviamente applicare l’arcotangente per avere la misura in gradi o radianti. Per esempio, dalla prima formula:
AB = AC · tgγ → γ = arctg(AB/AC)
Dimostrazione II teorema trigonometria sui triangoli rettangoli
Sappiamo che la tangente di un angolo non è altro che il coefficiente angolare della retta. Dovendo scrivere l’equazione della retta passante per l’origine e per il punto B possiamo scrivere:
y=mx+q

dove:
m = coefficiente angolare = tgγ
q = intercetta all’origine = 0
y = AB
x = AC
Ricomponendo l’equazione otteniamo la formula trigonometrica:
AB=tgγ · AC
Poiché l’angolo γ e β sono tra loro complementari, allora tgγ=cotgβ, per cui
AB= AC · cotgβ
Come si usano questi teoremi?
Le formule di trigonometria sui triangoli rettangoli vengono usate per risolvere problemi in cui vengono richieste le misure di cateti, angoli o ipotenusa. In particolare, per capire quali di questi 2 teoremi usare, basta valutare quali sono gli elementi noti:
Caso 1 – sono noti 2 cateti
In questo caso si possono trovare immediatamente gli angoli
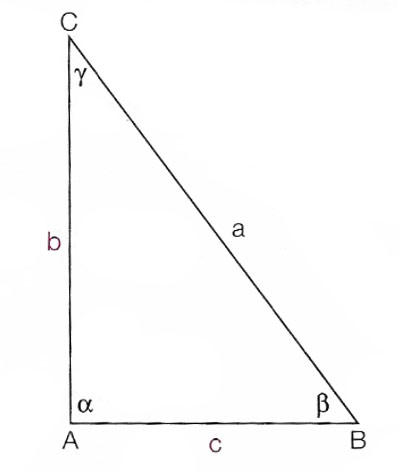
γ=arctg(AB/AC)
β=arctg(AC/AB)
Si può a questo punto calcolare anche l’ipotenusa sfruttando il primo teorema della trigonometria:
BC=AB/senγ
Ovviamente l’ipotenusa può anche essere calcolata con il teorema di Pitagora.
Caso 2 – sono noti 1 cateto e l’ipotenusa
In questo caso si applica subito la prima formula trigonometrica per trovare l’angolo:
AB=BC·senγ → γ=arcsin(AB/BC)
L’angolo β lo possiamo a questo punto calcolare semplicemente come β=90°- γ. L’ultimo cateto invece può essere calcolato con Pitagora.
Caso 3 – sono dati il cateto e un angolo acuto
Dato γ, possiamo subito calcolare β come angolo complementare: β=90°- γ. A questo punto posso calcolare anche l’ipotenusa come AB = senγ · BC. L’ultimo cateto possiamo infine ricavarlo con il teorema di Pitagora.
Caso 4 – sono noti l’ipotenusa e un angolo acuto
Anche in questo caso possiamo usare la formula inversa del primo teorema trigonometrico.
AB=senγ·BC → BC=AB/senγ
Avendo calcolato il cateto, possiamo calcolare il secondo angolo acuto come β=90°- γ, mentre l’ultimo cateto sempre con il teorema di Pitagora.
Conclusioni
I teoremi sui triangoli rettangoli della trigonometria permettono di poter risolvere completamente un triangolo. Sono sufficienti cioè 2 informazioni note (cateto, ipotenusa, angoli) per poter determinare tutto il resto.