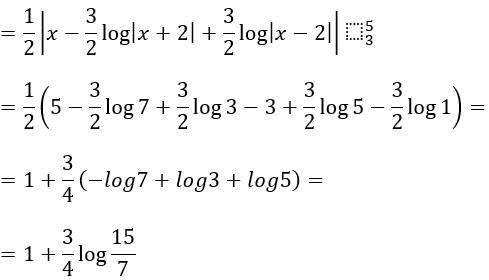Iniziamo questo importante teorema di analisi matematica parlando del concetto di media integrale. Data una funzione f(x) definita nell’intervallo continuo [a,b], la media integrale è il rapporto tra l’integrale definito tra a e b e la lunghezza dell’intervallo stesso.
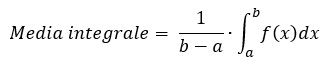
Enunciato del teorema della media integrale
Sia f una funzione continua nell’intervallo [a,b], allora esiste un punto f(c), tale che:
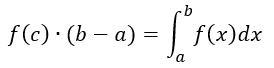
Significato geometrico
Partiamo dalle cose facili. Qual è il significato geometrico del teorema della media? Dalla lezione base sugli integrali forse ricorderai che questi non sono altro che l’area sottesa, cioè l’area nel piano cartesiano tra la funzione e l’asse delle ascisse.
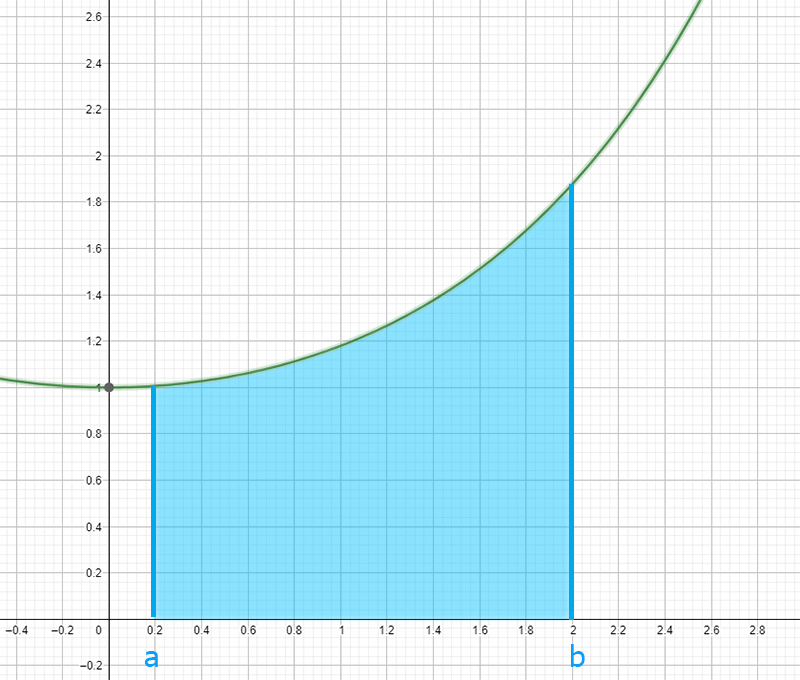
Vediamo invece cosa vuol dire il primo membro. Abbiamo un valore f(c) che è un’ordinata sul piano cartesiano (quindi un’altezza) che va moltiplicato per (b-a) (quindi una lunghezza). In pratica è come fare base per altezza, cioè è l’area di un rettangolo.
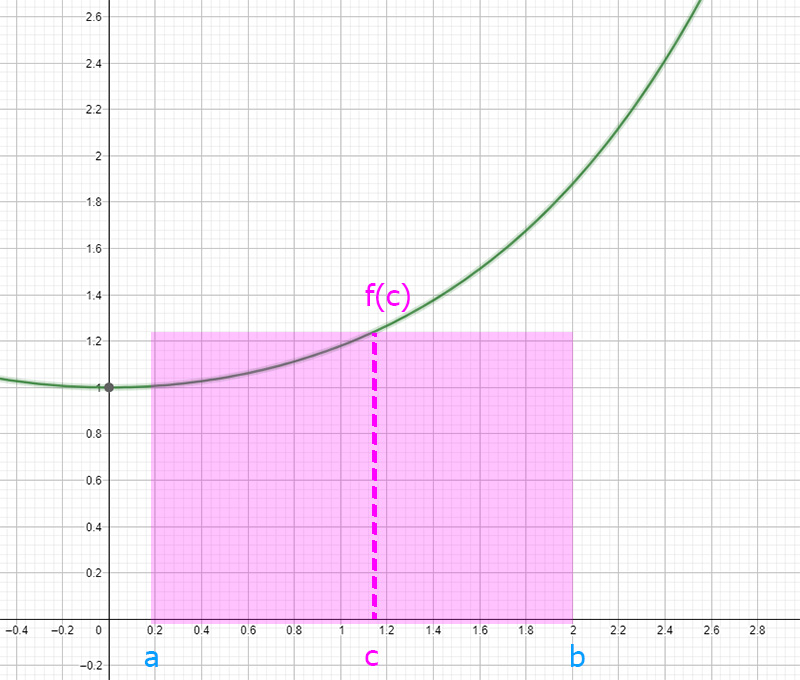
Il teorema della media integrale mette in evidenza l’uguaglianza di queste due aree.
Teorema della media integrale dimostrazione
Per enunciare e dimostrare correttamente il teorema è necessario conoscere il teorema dei valori intermedi e il teorema di Weierstrass. Niente paura, cerchiamo di rendere il tutto più semplice e veloce possibile.
Il teorema dei valori intermedi dice che se f(x) è continua nell’intervallo [a,b], allora la funzione assume tutti i valori compresi tra f(a) e f(b).
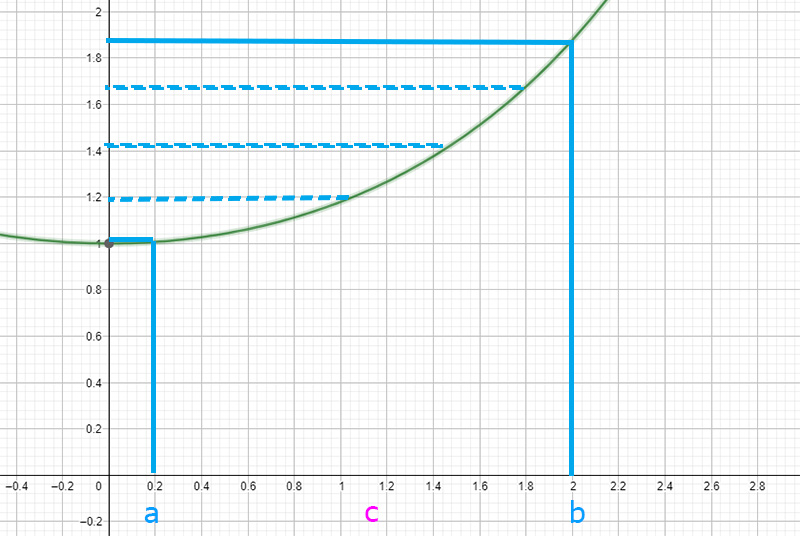
Come puoi vedere se la funzione è continua (cioè se la linea verde non ha interruzioni) tra a e b, allora proprio perché non ci sono interruzioni, ci sono tutti i valori compresi tra a e b.
Il Teorema di Weierstrass dice che se la funzione è continua sempre nello stesso intervallo, allora ammette un massimo e un minimo assoluti (cioè un punto più alto e un punto più basso, che puoi vedere facilmente sul grafico).
Possiamo quindi iniziare con la dimostrazione del teorema della media integrale. Per ipotesi diciamo che la funzione f(x) è continua tra a e b, per cui esistono un estremo inferiore m e un estremo superiore M. Vale quindi la relazione:
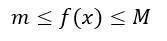
Per la proprietà di monotonia dell’integrale, possiamo applicare l’integrale ad ogni singolo membro e scrivere:
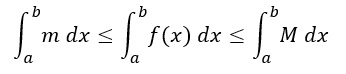
Poiché m ed M sono due costanti, possiamo portarli fuori integrali e risolvere l’integrale definito:
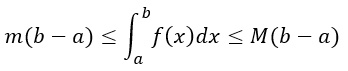
Ipotizzando che b>a, dividiamo tutto per (b-a), così da ottenere:
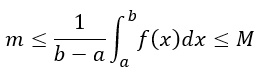
Per il teorema dei valori intermedi f deve assumere tutti i valori compresi tra m e M, per cui vuol dire che esiste certamente un valore (che chiamiamo f(c), per cui vale:
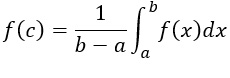
Basta a questi punto moltiplicare i due membri dell’equazione per b-a ed abbiamo dimostrato il teorema della media integrale.
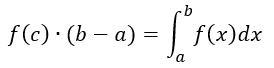
Teorema della media integrale esercizi svolti
Proviamo a risolvere insieme un esercizio di media difficoltà per studenti delle scuole superiori. Iniziamo subito con la traccia e poi con l’applicazione del teorema.
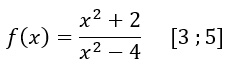
Applichiamo subito la definizione di teorema della media integrale:
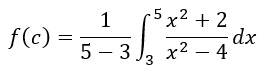
Per semplificarci la vita risolviamoci da parte l’integrale, come se fosse un semplice integrale indefinito, quindi senza estremi di integrazione. Li aggiungeremo dopo.
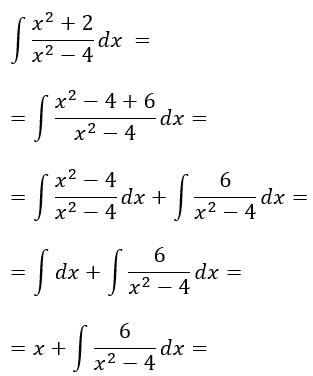
Risolviamo il secondo integrale con la tecnica delle razionali fratte con delta uguale a 0. Quindi prendiamo le costanti A e B e scriviamo:
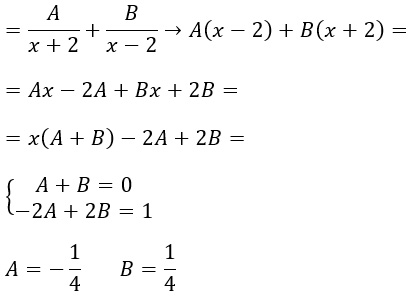
A questo punto possiamo tornare al nostro integrale e scrivere:
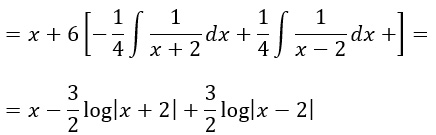
Possiamo a questo punto tornare all’integrale definito. Per cui scriviamo: