Il teorema dei seni stabilisce che in un generico triangolo, il rapporto tra un lato e il seno dell’angolo opposto resta costante.
Quando si applica e a che serve?
Il teorema del seno è valido per qualsiasi tipo di triangolo. Può essere quindi applicato sia ai triangoli rettangoli, che isosceli o equilateri.
Si tratta di uno dei più importanti teoremi di trigonometria, perché si rivela utilissimo negli esercizi e nei problemi sui triangoli in cui c’è bisogno di conoscere la misura di un angolo o di un lato.
Teorema dei seni: formula e definizione
Oltre alla prima definizione, che abbiamo dato all’inizio di questa lezione, il teorema del seno (o dei seni) si può anche definire in un secondo modo.
In ogni triangolo i rapporti tra le misure dei lati e il seno degli angoli opposti sono costanti ed uguali tra loro.
Dato il triangolo scaleno ABC, indichiamo con le lettere α β γ i tre angoli interni.
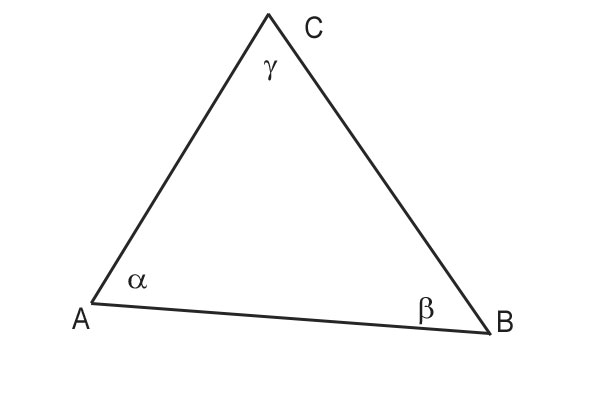
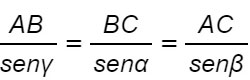
Dimostrazione del teorema dei seni
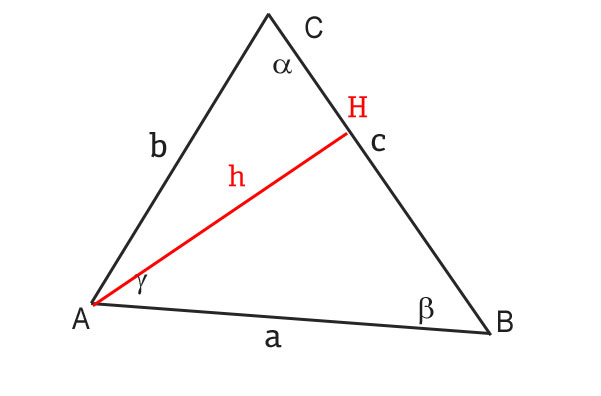
Proviamo ora a dimostrare la validità di questo teorema. Ridisegniamoci il generico triangolo, cercando di ricondurlo ad un problema già risolto. In trigonometria sappiamo risolvere bene i triangoli rettangoli, per cui tracciamo l’altezza, dividendo la figura in due triangoli rettangoli.
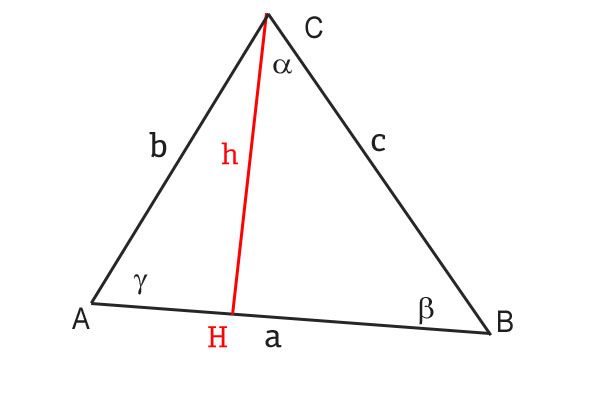
Andiamo ora ad applicare i teoremi sui triangoli rettangoli della trigonometria.
Dato il triangolo HCB, rettangolo in H, possiamo scrivere che:
h=c · sinβ
Dato il triangolo AHC, rettangolo in H, possiamo scrivere che:
h=b · sinγ
Uguagliando le due quantità otteniamo che:
b · sinγ = c · sinβ
Dividendo tutto per sinγ e sinβ, otteniamo:
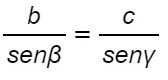
Rispetto alla formula del teorema dei seni che abbiamo visto ad inizio lezione, manca il lato a. Per ottenere quest’ultima parte, è sufficiente ridisegnare il triangolo con l’altezza relativa questa volta al lato c.
Ripetiamo gli stessi passaggi fatti nel caso precedente per cui, considerando i due triangoli rettangoli AHC e AHB, possiamo scrivere le relazioni:
-
h = a · sinβ
-
h = b · sinα
Da cui otteniamo infine:
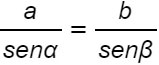
Possiamo a questo punto unire le due formule ottenute per ottenere la dimostrazione del teorema dei seni.
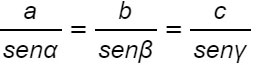
Esercizi svolti sul teorema dei seni
Problema 1
Determinare gli elementi incogniti di un triangolo ABC, sapendo che α=π/4, β=π/3 e b=8.
Svolgimento
Iniziamo a disegnare un generico triangolo, indicandone lati e angoli.
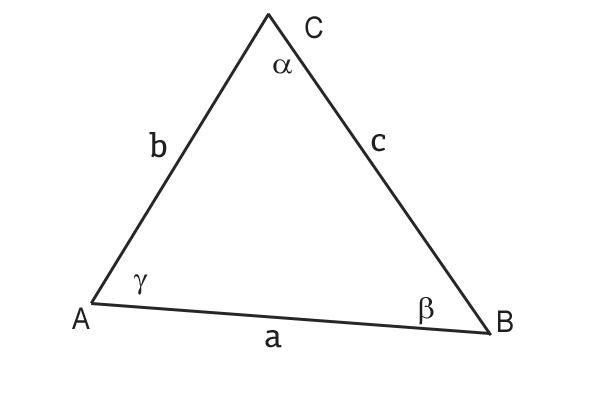
Determiniamo l’ampiezza dell’angolo γ. Ricordati che la somma degli angoli interni di un triangolo è pari a π. Il calcolo seguente può essere effettuato con gli angoli in gradi o in radianti, è indifferente.
γ = π – π/4 – π/3 = 5/12 π
Per il teorema dei seni si ha:
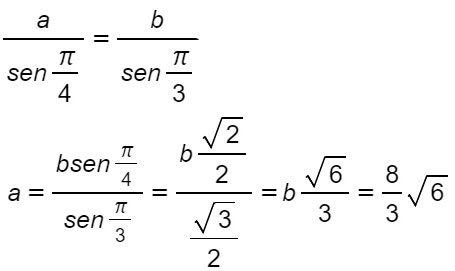
Sempre per lo stesso teorema ho:
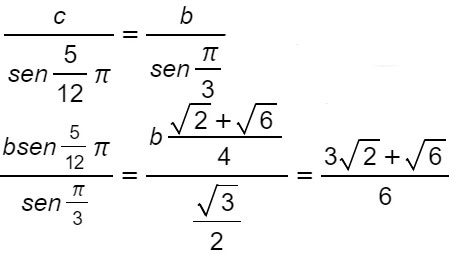
Esercizio 2
Nel triangolo ABC si ha: CB/CA=√6/2 e α=75°. Determiniamo l’ampiezza degli angoli γ e β.
Svolgimento
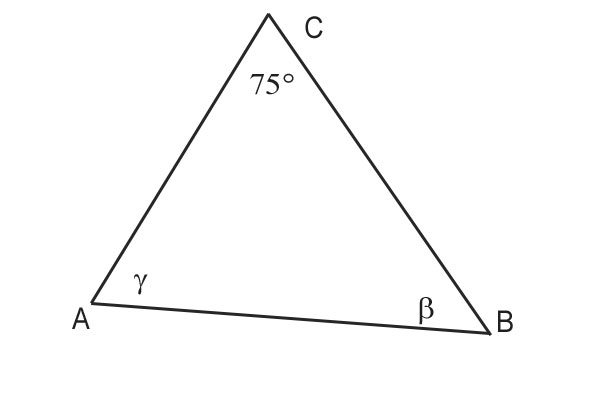
Per il teorema dei seni si ha:
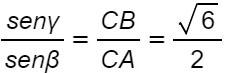
Poiché:
γ = 180° – 75° – β = 105° – β
Utilizzando le formule di sottrazione, allora possiamo scrivere:
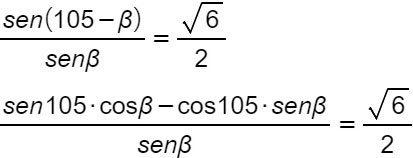
Poiché:
cos105° = cos 15° = (√6+√2)/4
Allora possiamo scrivere:
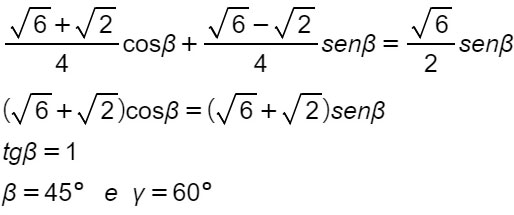
Conclusioni
Come hai potuto notare in questa lezione, l’applicazione e la formula del teorema dei seni è piuttosto semplice.
Bisogna tuttavia eseguire i calcoli senza avere fretta e ricordarsi che nel programma di trigonometria esistono tantissime formule che possono aiutarci a risolvere l’esercizio.