Uno studente in uno dei nostri corsi ci chiede un approfondimento sulla tangente di 45. “Come posso calcolare e soprattutto come posso ricavare e ricordarmi il valore della tangente di 45 gradi?”
All’interno della lezione sulla tangente di un angolo abbiamo parlato delle caratteristiche di questa particolare funzione goniometrica.
Tangente di 45 = 1
Il valore della tangente di 45, cioè tan45°, o in radianti tanπ/4, è uguale a 1
Quindi possiamo scrivere:
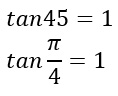
E’ generalmente è uno dei valori più semplici da ricordare in goniometria, per cui vale la pena impararlo a memoria, visto che non ci sono segni o radici.
Come posso ricordarmi quanto vale?
Se ricordi le relazioni fondamentali della goniometria, ricorderai che abbiamo definito la tangente come il rapporto tra seno e coseno.
Quindi possiamo scrivere che la tangente di 45 gradi è uguale alla divisione tra il seno di 45 e il coseno di 45.
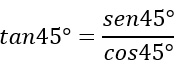
Sostituendo i risultati, abbiamo quindi:
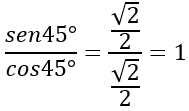
Poiché il seno e il coseno a 45 gradi sono uguali, allora il loro rapporto vale sempre 1. E’ proprio per questa ragione che la tangente di 45 gradi è pari a 1.
La tangente di 45 sul grafico
Ti ricordi la definizione grafica della tangente sugli assi cartesiani? Disegniamo la circonferenza goniometrica e su questa andiamo a staccare un angolo di 45 gradi (la semiretta in blu).
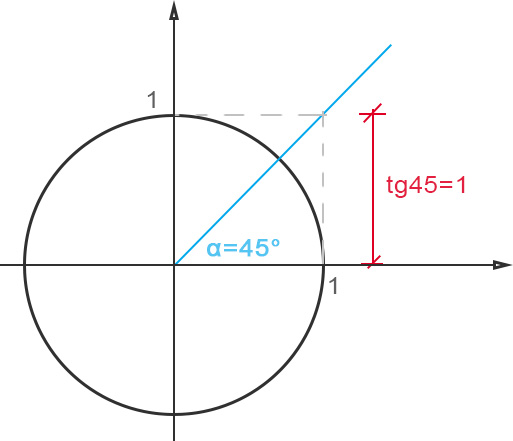
La tangente è il valore dell’ordinata che si genera dall’intersezione della semiretta dell’angolo (in blu) con la retta verticale x=1 (che passa cioè per il punto x=1 sull’asse delle ascisse).
Quando l’angolo è pari a 45°, questo valore di ordinata è proprio uguale al raggio della circonferenza goniometrica, cioè pari a 1.
Chiudiamo questa breve lezione di approfondimento chiedendoti un piccolo commento positivo nel caso in cui la spiegazione ti sia stata d’utile o se l’hai trovata chiara. Ci aiuterai a migliorare la qualità delle nostre lezioni e a fornirti ogni giorno nuovi contenuti di supporto. Buono studio!