La tabella goniometrica che troverai in questa lezione serve per individuare una specifica funzione goniometrica (seno e coseno, tangente e cotangente) per gli angoli che si trovano più frequentemente in trigonometria. Si tratta di una tabella completa da scaricare anche in formato pdf e che potrai stampare e portare sempre con te.
Tabella goniometrica completa
Come leggere la tabella di valori: nella prima colonna trovi l’angolo in gradi e radianti. Nella seconda colonna ci sono i valori del seno, poi il coseno, infine i valori di tangente e cotangente.
Angolo |
Seno |
Coseno |
Tangente |
Cotangente |
| 0° | 0 | 1 | 0 | ∞ |
| 30° | π/6 | 1/2 | √3/2 | √3/3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | √3/3 |
| 90° | π/2 | 1 | 0 | ∞ | 0 |
| 120° | 2/3 π | √3/2 | -1/2 | -√3 | -√3/3 |
| 135° | 3/4 π | √2/2 | -√2/2 | -1 | -1 |
| 150° | 5/6 π | 1/2 | -√3/2 | -√3/3 | -√3 |
| 180° | π | 0 | -1 | 0 | ∞ |
| 210° | 7/6 π | -1/2 | -√3/2 | +√3/3 | +√3 |
| 225° | 5/4 π | -√2/2 | -√2/2 | -1 | -1 |
| 240° | 4/3 π | -√3/2 | -1/2 | √3 | √3/3 |
| 270° | 3/2 π | -1 | 0 | -∞ | 0 |
| 300° | 5/3 π | -√3/2 | +1/2 | -√3 | -√3/3 |
| 315° | 7/4 π | -√2/2 | +√2/2 | -1 | -1 |
| 330° | 11/6 π | -1/2 | √3/2 | -√3/3 | -√3 |
| 360° | 2π | 0 | 1 | 0 | ∞ |
Scarica la tabella goniometrica in PDF
I valori presenti all’interno della tabella goniometrica possono essere individuati anche attraverso l’uso della calcolatrice, ma il problema è che questa non fornisce generalmente i risultati con i radicali e le frazioni, ma semplicemente con un numero con la virgola.
Come fare per impararli a memoria
Il dramma di tutti gli studenti che affrontano il programma di trigonometria è proprio imparare i valori della tabella goniometrica a memoria. Sono tanti e apparentemente non hanno alcun senso. Tuttavia c’è un metodo molto rapido per ricavare istantaneamente tutti i valori.
Come cambiano i segni
Hai presente la circonferenza goniometrica? E’ divisa in 4 spicchi, chiamati quadranti. Su ciascuno di questi seno e coseno assumono un segno differente. La tangente e la cotangente si ricavano dividendo i segni: segno del seno fratto segno del coseno.
- 1° (+;+) → Nel primo quadrante (in alto a destra) il seno e coseno entrambi positivi. Quindi anche tangente e cotangente positivi.
- 2° (+;-) → Nel secondo quadrante (in alto a sinistra) il seno è positivo, il coseno è negativo. Quindi tg e cotg sono negativi;
- 3° (-;-) → Nel terzo quadrante (in basso a sinistra) seno e coseno sono negativi. Quindi tangente e cotangente sono positivi;
- 4° (-;+) → Nel quarto quadrante (in baso a destra) seno positivo e coseno negativo. Quindi tangente e cotangente negativi.
Cosa succede nel primo quadrante
L’angolo 0 e l’angolo a 90° hanno funzioni goniometriche opposte. Quindi basta ricordare che a 0 gradi il seno vale 0, quindi il coseno vale 1. Quindi la tangente (seno/coseno) vale 0 e la cotangente infinito. A 90° gradi si invertono seno e coseno, tangente con cotangente.
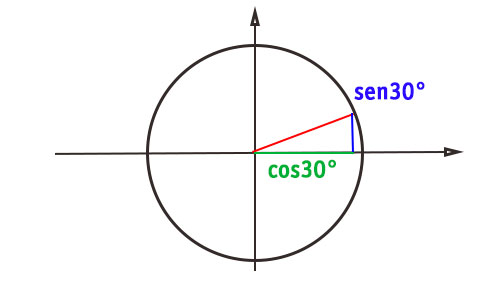
Nell’angolo di 30° il segmento del coseno è più lungo del segmento del seno. Dato che i valori in gioco sono 0,5 e radical 3/2 (circa 0,9), allora il seno è 1/2, il coseno è √3/2. Tangente e cotangente li ricaviamo al momento dividendo seno/coseno.
Approfondimenti: quanto vale il coseno di 30°?
A 60 gradi si inverte il valore del seno con quello del coseno, si inverte il valore della tangente con quello della cotangente.
A 45° devo semplicemente ricordarmi che seno e coseno sono uguali e pari a √2/2. Quindi tangente e cotangente sono pari a 1.
Cosa succede negli altri quadranti?
Hai visto la figura precedente con l’angolo di 30°? Ebbene prova a disegnare su un foglio di carta l’angolo da 150°, ti renderai conto che è identico all’angolo di 30°, ma ribaltato a destra. Quindi i valori della tabella goniometrica saranno gli stessi: il seno sarà 1/2 e il coseno radical 3/2. Ma attento ai segni, perché abbiamo detto che il coseno sarà negativo.
La stessa cosa si può dire anche con l’angolo da 120°. E’ il ribaltato sul secondo quadrante dell’angolo di 60°. Per cui i valori della tabella goniometrica sono gli stessi, ad eccezione dei segni. Questo ragionamento si ripete sia nel terzo che nel quarto quadrante.
Per approfondimenti: vai alla spiegazione sugli archi associati.
Conclusioni
In questa lezione hai imparato che esiste una tabella goniometrica con tutti i valori delle funzioni seno, coseno, tangente e cotangente stampati. Abbiamo inoltre visto che non è necessario impararla a memoria ma che, con un po’ di astuzia e di esercizio, si possono ricavare al momento tutti i valori di cui abbiamo bisogno.
E’ vero che serve un po’ di esperienza in materia, per cui ti consigliamo di fare tanti esercizi. Se anche in classe non dovessero assegnartene, tu non perdere tempo: esercitati! Per qualsiasi dubbio o chiarimento, scrivici un messaggio nei commenti.