Studio del segno di una funzione – come calcolare la positività di una funzione

Lo studio del segno di una funzione, detto anche positività di una funzione, è una tecnica di calcolo che permette di individuare quelle zone del grafico dove la curva studiata sta al di sopra o al di sotto dell’asse delle x.

Generalmente si effettua lo studio del segno della funzione subito dopo il calcolo del dominio, perché ciò permette di escludere rapidamente della vaste zone del grafico. Infatti attraverso l’analisi della positività è possibile andare ad eliminare dal disegno quelle zone sicuramente non attraversate dalla funzione.

Definizione di segno di una funzione

Immaginiamo di avere una generica funzione f:D⊆R, cioè data una curva f di dominio D appartenente al campo dei numeri reali. Per la definizione di funzione sappiamo che ad ogni valore di x corrisponde un unico valore di y, per cui y=f(x).

Questo significa che assegnando un valore alla x, otteniamo la y di conseguenza. Qual è il segno assunto dalla y in questo caso? Positivo o negativo? A questa domanda si risponde attraverso lo studio del segno di una funzione.

A che cosa serve lo studio del segno?

Sostanzialmente la positività di una funzione permette suddividere l’asse cartesiano, e quindi il grafico da realizzare, in delle aree con un segno specifico: più (+) o meno (-). Alla fine dei calcoli si può:

• ottenere un intervallo in cui la funzione è positiva, cioè si trova sopra l’asse delle x, quindi primo o secondo quadrante.
• ottenere un intervallo in cui la funzione è negativa, cioè si trova sotto l’asse delle x, quindi terzo o quarto quadrante.

Come studiare il segno di una funzione

Lo studio della positività della funzione è davvero semplice dal punto di vista concettuale, perché si calcola semplicemente imponendo la condizione:

f(x)>0

Si tratta quindi di andare a risolvere una disequazione. Lo studio del segno di una funzione è difficile solo se la funzione è particolarmente complessa. Risolvendo questa disequazione otterremo degli intervalli da sistemare poi sul grafico. Tutto ciò ti sarà molto più chiaro negli esempi che vedremo tra poco.

Segno di una funzione polinomiale

Il caso più semplice da analizzare riguarda lo studio del segno di una funzione polinomio del tipo y =axⁿ+bx^n-1+…+z

Esempio

Studiare il segno della funzione y=x²+4x+3

La condizione per lo studio del segno è y=x²+4x+3 > 0, per cui tutto quello che bisogna fare è risolvere una disequazione di secondo grado. Ecco come fare:

x²+4x+3 > 0 → la formula col delta è:

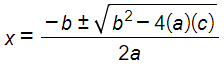
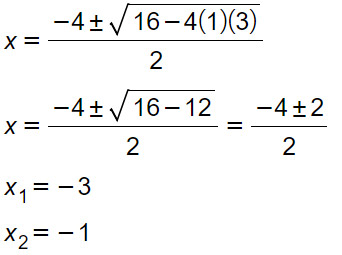
A questo punto essendo il verso e il primo coefficiente concordi si prendono soluzioni esterne, cioè il risultato è:

x<-3 U x>-1

Questa non è altro la soluzione dello studio del segno della funzione polinomiale. Non ci resta che mettere su grafico i valori ottenuti.

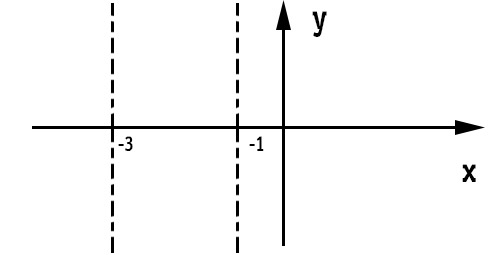
Come puoi vedere dal grafico abbiamo tirato degli assi in corrispondenza delle estremità dell’intervallo individuato. Come detto all’inizio, lo studio del segno di una funzione ci indica quali sono i valori per cui la curva è positiva (quindi sopra l’asse x). Ciò significa che:

• quando x<-3 siamo sicuri che la funzione si trova sopra (per cui la zona inferiore di grafico si può cancellare)
• quando x>-1 siamo sicuri che la funzione si trovi sopra (per cui anche questa zona si può eliminare)
• in tutti gli altri valori sono sicuro che la funzione si trova sotto (per cui posso cancellare la zona superiore del grafico).

Quindi il grafico ottenuto dallo studio del segno diventa:

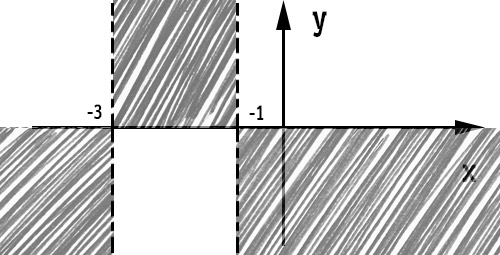
Attraverso queste cancellazioni abbiamo così ottenuto delle zone del grafico in cui passa la funzione. Dallo studio del segno possiamo quindi dedurre che in corrispondenza di x=-3 o x=-1 possono esserci dei punti di intersezione con gli assi o degli asintoti, a seconda del dominio e dello studio dei limiti.

Studio del segno di una razionale fratta

Inizia leggermente a complicarsi il calcolo visto che viene introdotto un denominatore. Per cui non bisognerà più risolvere una semplice disequazione razionale, ma una razionale fratta. Vediamo subito un esercizio svolto.

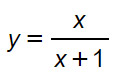
Applichiamo subito la regola vista in alto per lo studio del segno, per cui possiamo scrivere:

x>0
x+1>0 → x>-1

A questo punto inseriamo i valori sul grafico di questo falso sistema.

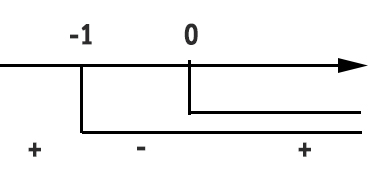
Poiché si prendono i valori positivi, il risultato sarà x<-1 U x>0. Questo è anche il risultato dello studio del segno della funzione, per cui possiamo completare il grafico finale. Anche in questo caso andremo ad eliminare (annerendole) la parte inferiore del grafico nell’intervallo trovato dal risultato. In tutto il resto si elimina sopra.

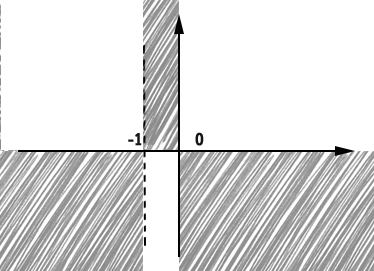
Studio del segno di una funzione irrazionale

In questo caso è importante avere una buona conoscenza sui metodi risolutivi delle disequazioni irrazionali. In caso contrario potremmo trovarci in difficoltà a risolvere le radici che si presenteranno per calcolare la positività della funzione.

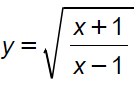
In questo caso dobbiamo studiare il segno di una funzione irrazionale fratta. Senza farci prendere dal panico per la presenza della radice, semplicemente applichiamo quanto visto fino ad ora, ovvero y>0.

Cerchiamo di essere furbi. Abbiamo una radice quadrata: hai mai visto una radice quadrata che come risultato da un numero negativo? NO! Questo perché la radice quadrata è una funzione sempre positiva, per cui la funzione si trova sempre sopra l’asse delle ascisse.

ATTENZIONE: in questo esercizio non è stato richiesto, ma la funzione ha ben due condizioni al dominio. Una disuguaglianza dovuta dalla presenza della radice (x+1)/(x-1)>0 e la condizione dettata dalla presenza del denominatore x≠+1. Questi valori devono essere cancellati anche dal grafico.

Studio del segno di una funzione logaritmica

In questo caso è importante conosce le nozioni base delle equazioni logaritmiche. Vediamo subito un esempio di positività di funzione logaritmica. In questo esercizio inseriamo anche lo studio di funzione, visto che generalmente nei grafici dello studio del segno ha una sua influenza.

y=log(x+1)

Ricordati che anche in questo caso è necessario calcolare il dominio, cioè x+1>0 → x>-1. Per quanto riguarda lo studio del segno vale sempre la stessa regola:

log(x+1)>0 → e^log(x+1)>e⁰ → x+1>1

x>0

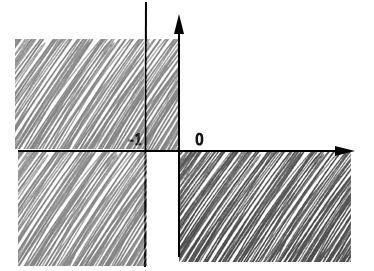
Possiamo inserire il risultato sul grafico eliminando già i valori esclusi dal dominio (cioè si cancella tutto ciò che si trova prima di -1 che potrebbe essere un asintoto verticale)

Studio del segno di una funzione esponenziale

Per poter risolvere questo caso, è importante avere una buona conoscenza sulle equazioni esponenziali. Vediamo subito un esempio concreto su come si procede:

y=e^x-1
y>0 → e^x-1>0 →  e^x>+1 → ln(e^x)>ln(+1) → x>0

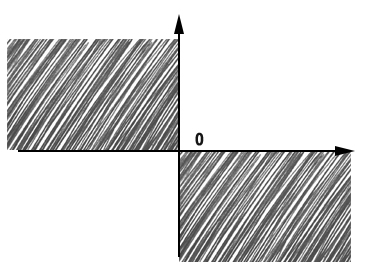
Il grafico in questo caso è estremamente semplice da realizzare, visto che si cancella la parte bassa del grafico in corrispondenza di x>0. Tutto il resto si cancella sopra.

Studio del segno di una funzione trigonometrica

Per poter risolvere questo caso è necessario sapere come si risolvono le disequazioni goniometriche. Vediamo come procedere con i calcoli in questo caso. Il dominio della funzione seno che vedrai dalla traccia include tutto R per cui non ci sono punti o zone di discontinuità.

y=sinx-1/2

sinx-1/2>0 → sinx>+1/2

Nella lezione sulla funzione seno abbiamo visto il grafico della sinusoide. Come puoi vedere dall’immagine in basso, il seno è maggiore di -1/2 per valori di x compresi da 0 a 210° e da 330° a 360°. Sul grafico finale andremo ad inserire proprio questi valori

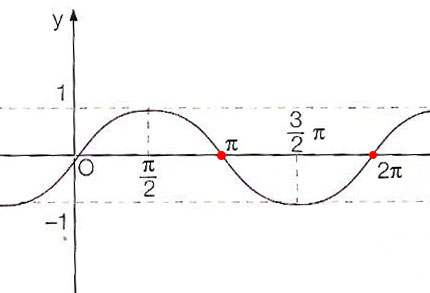
0<x<220° U 330°<x<360°