Simmetria assiale: formule ed esercizi svolti

In questa lezione cercheremo di capire che cos’è la simmetria assiale. Oltre ad analizzare la definizione, vedremo in maniera semplice che significa avere a che fare con la simmetria rispetto ad una retta. Troverai nel testo tanti esempi ed esercizi svolti di approfondimento, così da semplificare ulteriormente gli appunti.

Simmetria assiale definizione

La simmetria assiale rispetto ad una generica retta r è la trasformazione geometrica che a ogni punto di P fa corrispondere in punto P’ nel semipiano opposto rispetto a r e tale che r sia l’asse del segmento PP’. Per cui r passa per il punto medio di PP’ e PP’ è perpendicolare ad r.

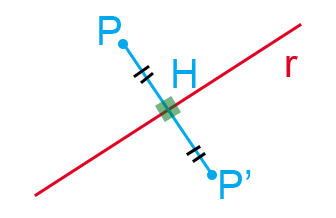
Cerchiamo di semplificare questa definizione. La simmetria assiale fa parte delle trasformazioni geometriche chiamata isometria, perché conserva le misure. Considerando la generica retta r, che chiameremo asse di simmetria, per disegnare il punto P’ con simmetria assiale rispetto a P, bisogna:

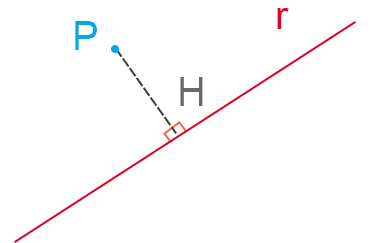
• disegnare la perpendicolare di P rispetto a r. Dalla loro intersezione individuiamo il punto H.

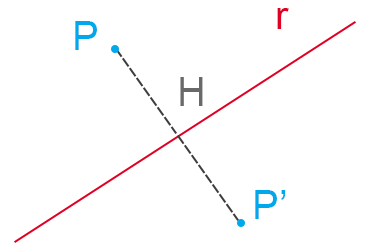
• Prolungare il segmento appena tracciato della lunghezza PH così da individuare P’. In questo modo avremo che PH=PH’.

ESEMPIO
Nel triangolo isoscele c’è simmetria rispetto all’altezza relativa alla base.

Proprietà

PROPRIETA’ 1 – La simmetria assiale è un’isometria. Per dimostrarlo, consideriamo due generici punti A e B e e la retta r. Da A e A’ tracciamo le perpendicolari AC e A’C’ alla retta per B e B’.

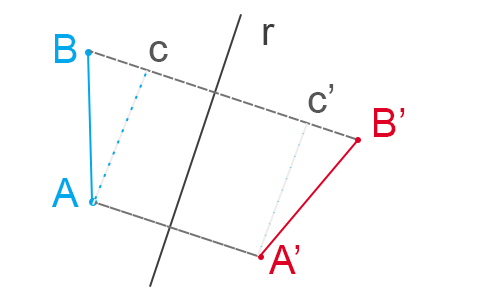
I triangoli rettangoli ABC e A’B’C’ sono congruenti perché hanno i lati congruenti. Quindi AB=A’B’.

PROPRIETA’ 2 – La simmetria assiale è una trasformazione involutoria, cioè facendo la sua inversa si torna nella posizione di partenza. In parole povere, “specchiando” un punto P si ottiene il punto P’. “Specchiandolo” di nuovo, cioè applicando la simmetria assiale composta alla prima trasformazione, si ottiene nuovamente il punto P.

PROPRIETA’ 3 – Tutti i punti dell’asse di simmetria sono punti uniti della trasformazione. Questo vuol dire che il simmetrico del punto P appartenente all’asse r è P’ coincidente proprio con P. Quindi l’asse di simmetria è una retta unita.

Simmetria assiale formule

Simmetria rispetto ad una retta parallela all’asse y

Consideriamo come asse di simmetria la retta verticale di equazione x=a. Dato il punto generico P(x,y), il punto P'(x’,y’) è il corrispondente di P se vale la formula:

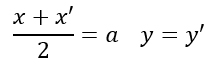
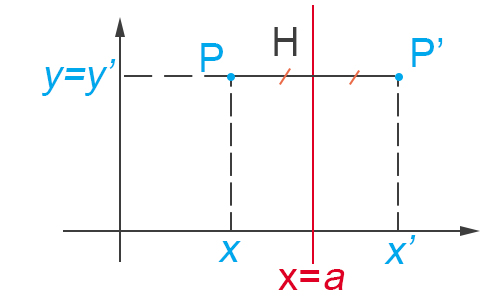
Come puoi vedere la y resta invariata, per cui y=y’. Per quanto riguarda la x invece, essendo x=a il punto medio, allora deve valere la formula (x+x’)/2. Per cui applicando la formula inversa per trovare x’, la simmetria assiale nel piano cartesiano si può esprimere come:

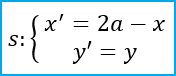
Simmetria rispetto ad una retta orizzontale

Ripetiamo quanto visto nel caso precedente facendo riferimento all’equazione della retta orizzontale. Dato il piano cartesiano Oxy e la retta parallela all’asse x di equazione y=b, per cui la x resta costante, cioè x=x’, mentre la b è il punto medio di y e y’. Per cui vale la formula:

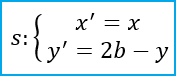
Simmetria rispetto alle bisettrici dei quadranti

Si dimostra che due punti con simmetria assiale rispetto ad una retta y=x (bisettrice I e III quadrante) hanno coordinate scambiate tra di loro. Per cui se P ha coordinate (x,y), allora P’ ha coordinate (y,x). Per la bisettrice del II e IV quadrante basta aggiungere un segno meno.

Simmetria rispetto ad una retta y=mx+q

Generalmente nella scuola primaria o al liceo difficilmente si incontra, ma per completezza la riportiamo tra le simmetrie nel piano cartesiano. Data quindi una generica retta di equazione y=mx+q, il simmetrico P'(x’,v’) deve appartenere a una retta perpendicolare a r e P e P’ devono essere equidistanti da r.

Quindi per far valere la condizione di perpendicolarità, allora il coefficiente angolare di PP’ deve essere l’opposto del reciproco di m. Ciò si traduce in:

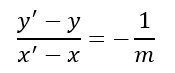
La seconda condizione invece ci dice che il punto medio del segmento PP’ deve appartenere alla retta r, quindi:

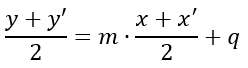
A questo punto si dimostra che, mettendo a sistema le due equazioni, si possono trovare le coordinate x’ e y’:

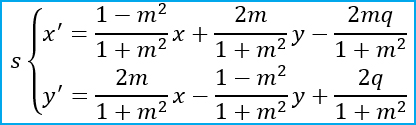
CASO PARTICOLARE – se la retta r passa per l’origine, allora la sua equazione diventa y=mx. Ricordandoci che la tangente di un angolo è il coefficiente angolare m, la formula finale si semplifica notevolmente.

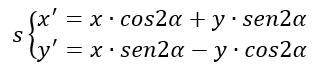
Esercizi svolti

Studia la seguente simmetria assiale:

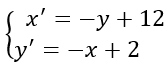
Poiché né la x né la y si conservano nelle loro trasformate x’ e y’, non si tratta di una simmetria rispetto a rette parallele agli assi cartesiani. Utilizziamo quindi la formula per la simmetria assiale rispetto alla generica retta y=mx+q (sì, quella più lunga e tosta). Facciamo un confronto tra la formula e la nostra traccia per trovare le due incognite del problema, cioè m e q, per cui ci servono 2 equazioni.

Considerando ad esempio la prima riga della formula notiamo che nel nostro caso non abbiamo il termine x, per cui possiamo imporre tutto il suo coefficiente pari a 0. Abbiamo così trovato la prima equazione!

Notiamo inoltre che il termine noto è pari a 12, per cui possiamo scrivere il termine noto della formula pari proprio a 12. Abbiamo così trovato la seconda equazione. Mettiamole entrambe in un semplice sistema di primo grado.

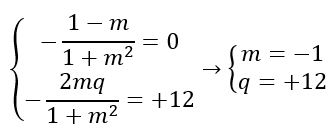
Conclusioni

Se la lezione ti è stata utile o hai ancora dei dubbi o delle curiosità, lascia un commento in basso. Un tuo feedback positivo ci aiuta a migliorare ogni giorno la qualità delle nostre lezioni.