Seno iperbolico – senh(x) – definizione, formula e proprietà

Il seno iperbolico si indica generalmente con sinh(x) o senh(x) e appartiene ad una famiglia di funzioni particolari con proprietà simili alle funzioni goniometriche. La differenza principale sta nel fatto che mentre seno e coseno si ricavano dalla circonferenza goniometrica, il seno iperbolico e il coseno iperbolico si ricavano dal grafico dell’iperbole.

Definzione

La prima domanda a cui bisogna rispondere è: che cos’è il seno iperbolico?

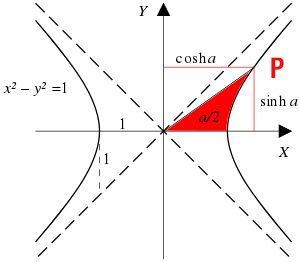
Seno iperbolico definizione

Data un’iperbole equilatera di equazione X²-Y²=1 centrata sull’origine degli assi cartesiani e dato un angolo α, andiamo a considerare il settore iperbolico disegnato in rosso di area α/2. Questo determina sull’iperbole un punto P. Si definisce seno iperbolico l’ordinata del punto P.

sinh(x)=y_P

Le funzioni iperboliche vengono definite attraverso l’uso di funzioni esponenziali con base naturale. In questo caso possiamo scrivere che:

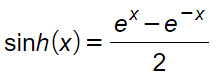
Proprietà

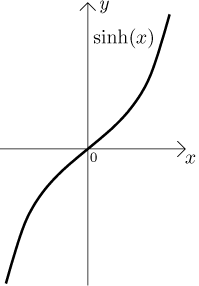
Grafico del seno iperbolico

Al grafico disegnato nel piano cartesiano si arriva facilmente effettuando un normale studio di funzione che riportiamo di seguito.

Dominio

Dalla definizione che abbiamo appena espresso, possiamo individuare il campo di esistenza della funzione seno iperbolico. Il dominio degli esponenziali e^x e e^-x è tutto R. Per cui possiamo scrivere che il dominio è

D: ∀ x∈R
o anche
D=(-∞;+∞)

Il seno iperbolico è una funzione continua in tutto R

Simmetrie

Poiché vale l’uguaglianza f(x)=-f(-x), cioè
e^x – e^-x=-(e^-x – e^+x)
allora la funzione seno iperbolico è dispari, cioè simmetrica rispetto all’origine degli assi cartesiani.

Intersezione con gli assi

Si impone come sempre si fa nello studio di funzioni, sinh(x)=0. Moltiplicando subito primo membro e secondo membro per 2, si ottiene:

e^x – e^-x=0

e^x = e^-x 

x=-x → 2x=0 → x=0

Quindi abbiamo scoperto che il seno iperbolico di 0 fa 0. sinh(0)=0

Studio del segno e positività

Si impone il sinh(x)>0. Per cui passando alla definizione di esponenziali e moltiplicando tutto per 2 otteniamo:

e^x – e^-x>0

e^x > e^-x

x>-x

2x>0

x>0

Quindi la funzione seno iperbolico è positiva per x>0, mentre è negativa per x<0.

Limiti agli estremi

I limiti del seno iperbolico a meno infinito e più infinito sono rispettivamente meno infinito e più infinito.

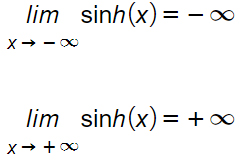
Derivata

Così come accadeva con il seno, la derivata del seno iperbolico è pari al coseno iperbolico.

d(sinhx)=coshx

Integrale

Riprendendo ancora l’analogia con il seno, l’integrale del seno iperbolico è pari al coseno iperbolico cambiato di segno.

∫sinh(x)dx=-cosh(x)+k