In questa lezione vedremo come si calcola l’equazione della retta passante per due punti noti nel piano cartesiano. Si tratta di una delle formule che si studiano nella prima parte del programma di geometria analitica e permette di risolvere numerosi esercizi.
Con la formula della rette per due punti è possibile determinare l’equazione di una retta che passa per 2 punti di cui sono note le coordinate cartesiane.
A fine lezione vedremo alcuni esercizi guida commentati passo passo, così da facilitare l’applicazione della regola studiata.
Equazione retta passante per due punti
Vediamo subito come trovare l’equazione di una retta che passa per due punti A e B di cui sono note le coordinate.
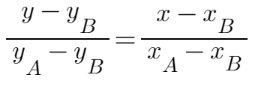
dove i due punti sono A(xA, yA) e B(xB, yB).
Osservazioni e consigli
E’ possibile osservare che l’equazione è formata da un’uguaglianza tra due frazioni. Il primo termine al numeratore del primo e del secondo membro è senza pedice.
La y e la x che vedi senza il pedice vanno lasciate sotto forma di lettera
Questo perché x e y sono le variabili dell’equazione della retta y=mx+q finale che otterremo.
La formula della retta passante per due punti vista ora, è valida solo quando xA è diverso da xB e quando yA è diverso da yB. In parole povere non si può applicare nel caso in cui si abbia un retta orizzontale o una retta verticale.
Retta per due punti orizzontale/verticale
- Retta verticale: x=k → nel caso in cui i due punti abbiano stessa ascissa. L’equazione della retta sarà l’ascissa stessa che hanno in comune.
Esempio:
Calcolare l’equazione della retta che passa per i punti A(3;2) e B(3;0)
Svolgimento: In questo caso l’equazione della retta sarà x=3.
- Retta orizzontale: y=k → nel caso in cui siano uguali le ordinate dei due punti, allora l’equazione della retta sarà y uguale all’ordinata stessa.
Esempio:
Calcolare la retta passante per i due punti A(0;1) B(5,1)
Svolgimento: in questo caso l’equazione sarà invece y=1.
Dimostrazione formula retta per 2 punti
Poiché la retta passa per i due punti A e B, vuol dire che questi due appartengono alla retta. Imponiamo dal punto di vista matematico questa appartenenza, andando a sostituire in due equazioni separate le coordinate di A e B nell’equazione della retta esplicita.
y=mx+q
- Sostituisco le coordinate di A: yA=m·xA+q
- Sostituisco le coordinate di B: yB=m·xB+q
Dato che la retta passa per i due punti contemporaneamente, vuol dire che ho un sistema di primo grado che posso risolvere con la tecnica della sottrazione per trovare le incognite m e q.
yA=m·xA+q –
yB=m·xB+q =
____________
(yB-yA) = m (xB-xA)
Posso ricavare la prima incognita m, ovvero il coefficiente angolare della retta passante per due punti:
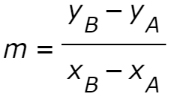
A questo punto posso sostituire in una delle due equazioni del sistema:
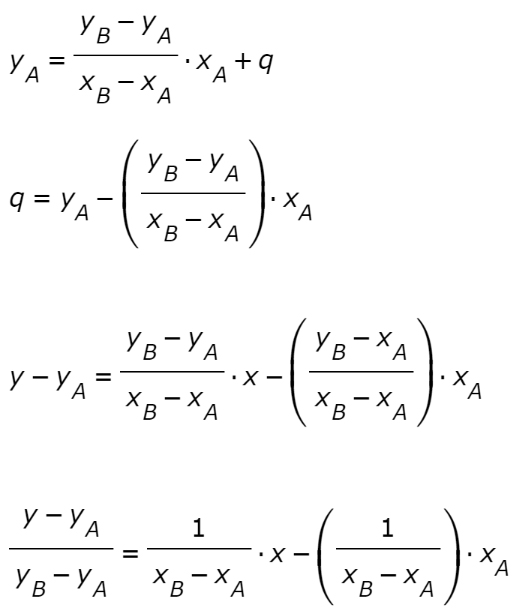
Nell’ultimo passaggio abbiamo semplicemente diviso tutta l’equazione per yB-yA. A questo punto mettiamo in evidenza la parentesi tonda al secondo membro. In questo modo otteniamo la formula della retta per due punti.
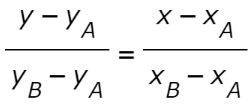
Esercizi svolti
Abbiamo capito, anche grazie alla dimostrazione l’equazione di una retta passante per 2 punti. Ora proviamo a svolgere assieme qualche esercizio guida.
Esercizio 1
Trovare l’equazione della retta passante per 2 punti A(-5;0) e B(3;2).
Svolgimento
Applichiamo semplicemente la formula vista.
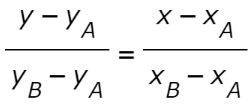
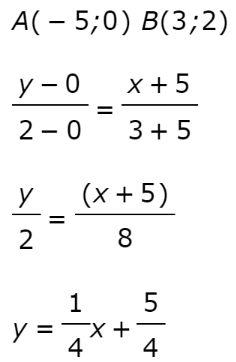
L’esercizio si è dimostrato molto semplice. Unica attenzione al doppio segno al secondo membro.
Esercizio 2
Calcolare l’equazione della retta per due punti A(0;0) e B(1/2, -3).
Svolgimento
Anche in questo caso è sufficiente andare a sostituire i numeri. Attenzione alla doppia frazione al secondo membro.
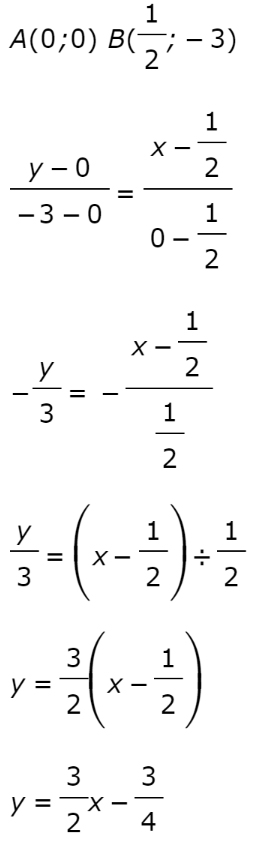
Conclusioni
Abbiamo visto che per trovare le rette per due punti servono sostanzialmente solo le coordinate dei punti stessi. Si tratta di un calcolo semplice su cui, però, bisogna fare attenzione ai segni.
La lezione si conclude, ma lasciamo spazio in basso alle considerazioni degli studenti. Se gli appunti sono stati utili e chiari, ti chiediamo di lasciare un commento positivo. Ci serve per migliorare la qualità delle lezioni e offrire sempre contenuti di qualità.
Se invece ci sono ancora dubbi o incertezze, siamo a disposizione per qualsiasi domanda. Buono studio.