I radicali in matematica vengono definiti come degli operatori (cioè che permettono di fare operazioni). Vengono espresse attraverso delle radici che hanno un indice intero. Le radici quadrate o più in generale i radicali mettono spesso in difficoltà gli studenti all’interno dei vari esercizi.
Proprio per questa ragione, abbiamo deciso di semplificare al massimo la lezione sui radicali, così da permettere davvero a tutti di comprenderne regole e proprietà. Iniziamo dalla definizione e da un esempio pratico di radice quarta.
Nell’esempio sopra vedi puoi vedere come si esprimono i radicali in matematica:
- 3 – viene chiamato coefficiente della radice;
- 2 – viene chiamato argomento della radice;
- 4 – viene chiamato indice di radice.
Le regole sui radicali sono abbastanza simili a quelle che abbiamo visto per le potenze. Si tratta quindi di poche semplici regole, utilissime tuttavia nella risoluzione degli esercizi. In questa lezione vedremo le proprietà dei radicali e alcune applicazioni concrete con esempi ed esercizi svolti.
Presta bene attenzione e magari segnati un appunto per ogni singola regola, perché in questa pagina troverai davvero tutto quello che ti serve per risolvere senza alcun problema gli esercizi contenenti operazioni tra radicali.
Regola sui radicali fondamentale – la semplificazione
Volendo costruire uno schema semplice su come risolvere i radicali, iniziamo dalla semplificazione, indicata dai testi come la fondamentale proprietà delle radici:
Moltiplicando l’indice della radice e l’esponente per uno stesso numero, il valore del radicale non cambia.
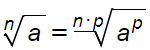
Questo significa che il numero che indica la potenza e il numero che indica la radice possono essere semplificati tra loro. Vediamo subito un esempio pratico:
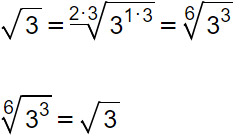
La regola vale anche al contrario. Ti capiterà spesso di incontrare, infatti, degli esercizi sui radicali in cui dovrai semplificare l’indice di radice con l’indice di potenza.
In questo esempio all’inizio abbiamo moltiplicato l’indice di radice 2 (il numero in alto a sinistra) e l’indice di potenza 1 per lo stesso numero, cioè per 3. In questo caso abbiamo moltiplicato, ma la regola vale anche per la divisione.
Operazioni con i radicali
La somma e la differenza non possono essere eseguite. Errore comune di molti studenti è pensare che √3+√7=√10. In realtà è sbagliato! Il risultato è: √3+√7, cioè si lascia tutto così com’è. Tieni questo concetto ben presente tra le proprietà dei radicali.
Le moltiplicazioni tra radicali
La moltiplicazione di due o più radicali aventi lo stesso indice di radice è un radicale avente lo stesso indice e per radicando il prodotto dei radicandi.
Approfondimento: la moltiplicazione di radicali – formule ed esercizi utili
Le moltiplicazioni tra radici sono tra le più semplici proprietà dei radicali. La regola vale solo se l’indice è lo stesso! Questa è l’unica cosa a cui bisogna prestare attenzione. Per risolvere i radicali con le moltiplicazioni è sufficiente moltiplicare i radicandi (cioè i numeri sotto radice). Vediamo con un esempio pratico:
Dal primo al secondo passaggio possiamo dedurre importantissima proprietà: è possibile scrivere le radici separatamente (radical due, radical tre e radical quattro) oppure inserirle sotto un’unica radice. La cosa importante che l’indice sia lo stesso, nel nostro esempio 3. Vediamo un altro caso concreto per capire bene questa regola sui radicali appena dedotta:
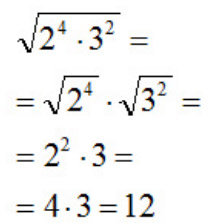
Da notare che i radicali sono spariti perché abbiamo semplificato indice di radice ed esponente per due, applicando la fondamentale proprietà sui radicali.
La divisione
Il quoziente di due radicali aventi lo stesso indice è un radicale avente lo stesso indice e per radicando il quoziente dei radicandi.
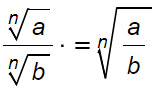La formula per risolvere i radicali tra loro divisi è molto semplice. E’ sufficiente infatti dividere i radicandi. La conseguenza di questa regola, come si può vedere anche dalla formula è che possiamo scrivere sia due radicali separati che sotto un’unica radice. Ecco un esempio:
Esempio di divisione tra radici
Da notare come negli esercizi sulle radici, è fondamentale cercare di esprimere i numeri in forma di potenze, così da poter provare poi a semplificare.
Potenze di radicali
Per elevare a potenza un radicale si eleva a potenza il radicando.
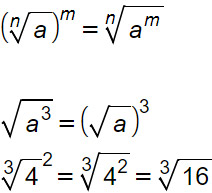Nei due esempi che ti abbiamo illustrato, puoi vedere che questa regola sulle potenze è estremamente semplice: basta fare la potenza del numero sotto la radice!
Radici di radici
Questa è la proprietà delle potenze che maggiormente mette in difficoltà gli studenti. Non c’è bisogno neanche di fare schemi semplici, perché è immediato:
La radice di un radicale è uguale ad un radicale che ha per indice il prodotto degli indici e per radicando lo stesso radicando.
Che tradotto significa: non ti fare troppi problemi, semplicemente moltiplica gli indici di radice e hai fatto, come puoi vedere nell’esempio:
Radici di radici con esempio
Nel caso in cui sotto la radice non ci sia solo un numero ma ad esempio un binomio, allora bisogna ricorrere alla regola sui radicali doppi.
Portare fuori radice ( e dentro la radice)
Il trasporto fuori dal segno di radice si esegue scomponendo al massimo i numeri ed applicando le regole viste in precedenza. In genere si procede riscrivendo il radicando in forma di potenza e semplificando con la radice. Vediamo subito un esempio pratico:
Come portare fuori radice…
In questo piccolo esercizio abbiamo scomposto il radicando e successivamente usato le proprietà delle potenze, in particolare la regola della moltiplicazione. Dalla singola radice siamo passati alle due radici moltiplicate e, semplificando ancora, abbiamo ottenuto il risultato finale.
Il trasporto di un numero dentro la radice è probabilmente anche più semplice. Il numero da portare sotto radice va elevato all’indice di radice e inserito nel radicando come se fosse una normale moltiplicazione. Ecco un esempio:
Esempio di come portare un numero sotto radice
Esempi
Per aiutarti a fare i tuoi esercizi di matematica avendo ben capito come risolvere i radicali, ti presentiamo i nostri esercizi svolti. Applicheremo in maniera rigorosa tutte le proprietà dei radicali.
Semplificare i radicali applicando le regole sulle radici
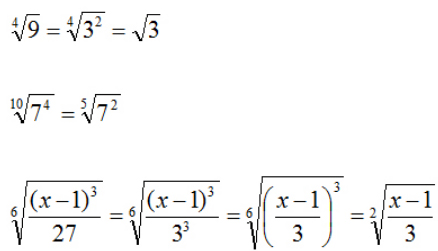
Nell’ultimo esercizio abbiamo cercato di ridurre il denominatore a una potenza e, avendo lo stesso esponente del numeratore, abbiamo portato tutto nella stessa parentesi ed infine semplificato.
Eseguire le seguenti moltiplicazioni tra radicali
Quest’esercizio ha una particolarità: gli indici di radice sono tutti diversi. Questo significa che non è possibile usare la regola sulle moltiplicazioni tra radicali! Per poterne usufruire è necessario prima fare in modo che tutti gli indici di radice siano uguale. Ciò è possibile con il calcolo del minimo comune multiplo tra gli indici:
mcm(2,3,4)=12
Per cui l’indice comune sarà 12. Moltiplico quindi indice ed esponente del primo radicale per 6 (l’operazione che abbiamo eseguito è stata mcm:indice=12:2=6). Con il secondo ho fatto mcm:3=4, per cui ho moltiplicato indice ed esponente per 4 e così anche nell’ultimo radicale rimasto. A questo punto ho ottenuto tre radicali con stesso indice di radice e posso applicare normalmente la regola sulle moltiplicazioni.
Eseguire le seguenti divisioni tra radicali
Anche nell’esercizio sulle divisioni tra radicali compare lo stesso problema precedente: non ci sono indici uguali. Proprio per questo l’esercizio è stato risolto come prima: calcoliamo il minimo comune multiplo tra gli indici, riduciamo tutti i radicali allo stesso indice di radice e poi eseguiamo la divisione normalmente.
Portare sotto radice il fattore esterno e, se possibile, semplificare i risultati
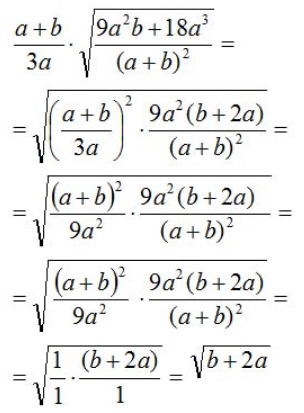
L’esercizio non è particolarmente complesso, basta che ti ricordi le scomposizioni dei polinomi, dato che abbiamo fatto una messa in evidenza totale.
Eseguire le operazioni tra radici e semplificare
Conclusioni
Con questa lezione abbiamo provato a fornirti uno schema semplice sui radicali, cercando di rispondere alle domande più frequenti degli studenti. Ti invitiamo comunque a risolvere altri problemi dalla nostra lezione Esercizi sui Radicali oppure puoi scaricare la simulazione del prof. Cantone.
Se la lezione ti è stata utile o se hai ancora dei dubbi sulle regole e proprietà dei radicali in matematica, lascia un commento sotto. Ci aiuterai a migliorare la qualità della lezione e a renderla sempre più vicina alle tue esigenze.
è spiegato molto bene…grazie mille mi hai dato una gioia in più : )
L’esempio della divisione tra radicali è sbagliata. Il mcm tra gli indici 4 e 2 è 4 quindi xalla seconda diviso y alla seconda.
Grazie della segnalazione,
abbiamo già provveduto ad effettuare la correzione. Continua a seguirci.
Lo staff
tutto chiaro ,grazie .mi pare pero` che il risulyato del penultimo esercizio sia radice di. b+2a ,o mi sbaglio?
MOLTO chiaro, semplice ecc.
esposizione molto chiara e sintetica .non lascia nessun dubbio