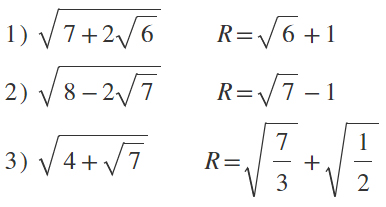Si chiamano radicali quadratici doppi, o semplicemente radicali doppi, quelle espressioni contenenti una radice e nel radicando una somma o una differenza tra un numero e una radice. La forma generica in cui puoi trovare una radice doppia è:
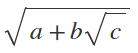 Radicali doppi con la somma |
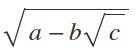 Radicali doppi con la differenza |
La prima operazione da svolgere
Prima iniziare a risolvere i radicali doppi è importante fare in modo non ci sia un coefficiente davanti la radice interna. Cioè la “b” delle formule in alto non va bene lì dov’è. Quindi la prima operazione è quella di portare il coefficiente sotto radice. Come? Inserendolo al quadrato con il simbolo “per” all’interno della radice. Facciamo subito un esempio con un esercizio tipo:
√(11-6√2)
In questo caso il 6 va inserito all’interno della radice. Lo si eleva al quadrato e lo si mette sotto radice:
=√[11-√(36·2)]=
=√(11-√72)
A questo punto siamo pronti per applicare la formula per risolvere le radici doppie.
Approfondimenti: regole e proprietà dei radicali
Formula radicali doppi
La formula risolutiva per i radicali quadratici doppi è:
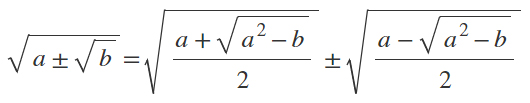
Considerazioni
Lo vedi il simbolo “più” “meno” ? Significa che la formula si può risolvere sia con il più che con il meno. Cioè se nel tuo esercizio sui radicali doppi hai un segno più, considererai nella formula il segno “+” tra le due radici. Se invece nel tuo esercizio c’è il segno “-“, allora nella formula andrai a considerare il segno meno. Facile vero?
Un consiglio per ricordarla
Così a prima vista la formula ti può sembrare difficile da ricordare, ma in realtà può facilitare la memorizzazione ricordandoti che si tratta della somma algebrica (cioè somma o differenza) di due radici.
All’interno di ogni radice trovi il primo termine sommato con una seconda radice interna all’interno della quale c’è il primo termine al quadrato meno il radicando della seconda radice. Il tutto fratto 2. Questa radice va sommata o sottratta ad una seconda radice, identica alla prima, ma con il segno interno cambiato.
Quando applicare la formula dei radicali doppi
La condizione fondamentale senza la quale gli esercizi non potrebbero essere svolti è che la quantità nel radicando sia maggiore o uguale di zero. Questo significa che se a2-b≥0 l’esercizio può essere risolto, altrimenti ti ritroveresti con una radice negativa, impossibile da svolgere nei numeri reali.
E’ importante inoltre che i numeri a e b siano dei quadrati perfetti, cioè la loro radice quadrata deve essere un numero intero. Se questa condizione non viene rispettata allora il metodo dei radicali doppi che siamo vedendo in questa lezione potrebbe solo complicarti le cose.
Esercizio svolto
Torniamo dall’esempio precedente che avevamo interrotto a metà:
√(11-6√2)
Senza ripetere i passaggi fatti prima possiamo dire che questa radice è uguale a:
=√(11-√72)
Applichiamo la formula dei radicali doppi con la sottrazione:
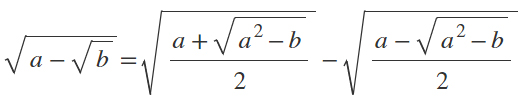
Iniziamo individuando chi sono a e b. Attenzione al secondo coefficiente: si tratta del numero senza radice.
a=11 b=72
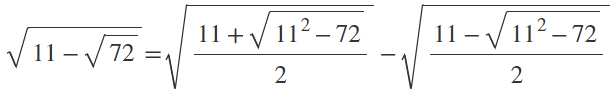
A questo punto si tratta semplicemente di fare qualche calcolo algebrico.
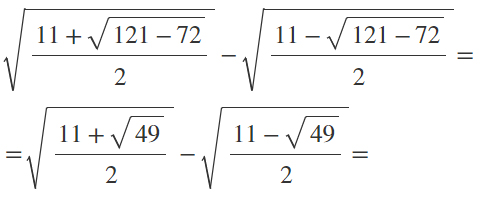
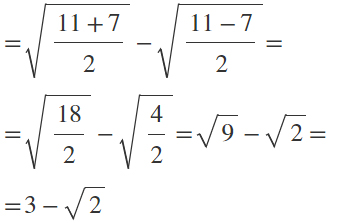
Come hai potuto vedere non è difficile semplificare i risultati doppi e ridurli in una forma più semplice ed accessibile. Ti consigliamo comunque di fare qualche esercizio così da verificare che ti sia effettivamente tutto chiaro. Verifica di essere in grado di applicare la formula svolgendo i seguenti esercizi.
Radicali doppi esercizi
Trasforma i seguenti radicali quadratici doppi nella somma algebrica di radicali semplici, quando possibile.