x0 è un punto di accumulazione per l’insieme A se in ogni intorno di x0 cadono infiniti elementi di A.
In questa lezione vedremo che cosa sono i punti di accumulazione, un concetto non sempre facile per gli studenti, ma che serve per introdurre poi il concetto di limite.
Per poter capire che cos’è un punto di accumulazione è necessario sapere cosa si intende per sottoinsieme e per intorni di un punto.
Punto di accumulazione definizione
Sia A un sottoinsieme di R, cioè A⊆R, un numero reale x0 si definisce punto di accumulazione di A se ogni intorno di x0 contiene almeno un elemento di A diverso da x0.
Su altri libri di testo viene anche scritto che x0 si dice punto di accumulazione quando per ogni intorno di x0 cadono infiniti elementi di A.
Le due definizioni sono perfettamente analoghe e possono essere utilizzate entrambe senza alcuna differenza.
Possiamo scrivere in termini matematici:
x0 è un punto di accumulazione per A⊆R se
![]()
Alcune rapide considerazioni
Nella definizione di punto di accumulazione ci sono alcune parole su cui è importante prestare la giusta attenzione.
Infatti affinché x0 possa definirsi punto di accumulazione è necessario che qualsiasi suo intorno contenga i punti del sottoinsieme A. Questo significa che non basta trovare un generico intorno che soddisfi la definizione, ma è importante che la proprietà valga per ogni intorno di x0.
Ci rendiamo perfettamente conto che per uno studente i punti di accumulazione possono risultare astratti e difficili da comprendere. Proprio per questa ragione vediamo di seguito alcuni esempi svolti e commentati.
Esempi sui punti di accumulazione
ESEMPIO 1
Iniziamo studiando la funzione seguente:
![]()
Andiamo a determinare il dominio della funzione D. Poiché la funzione è composta da due funzioni irrazionali, è sufficiente imporre il maggiore e uguale per ogni radicando.
Si ottengono così due disequazioni di secondo grado che si risolvono molto agevolmente e che poi vanno unite.
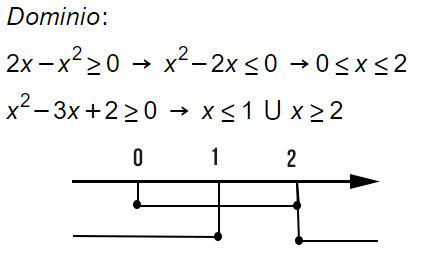
Dall’unione delle due disequazioni si ottiene la soluzione:
0≤x≤1 U x=2
Consideriamo ora D come sottoinsieme dei numeri reali R.
Tutti i punti che si trovano nell’intervallo [0;1] possono essere chiamati punti di accumulazione, perché qualsiasi intervallo se ne consideri all’interno, questo ricade sempre all’interno del dominio D. Vediamo graficamente di essere più chiari.
Nell’intervallo del dominio D (sottoinsieme di R) prendiamo in generico punto x0 che disegniamo in blu per chiarezza grafica.
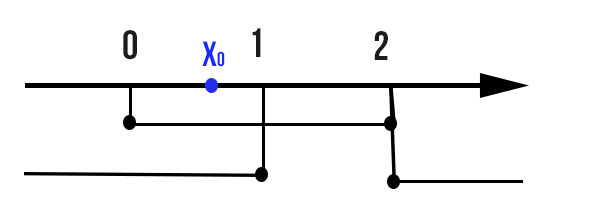
A questo punto proviamo a determinare un generico intervallo piccolo a piacere (quindi non molto grande) e disegniamolo in arancione.
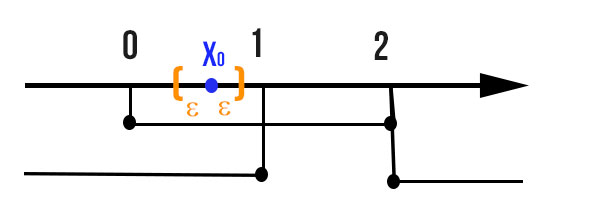
Tutti i punti dell’intorno disegnato in arancione ricadono nel sottoinsieme D. Per cui x0 è un punto di accumulazione. Puoi provare a disegnare qualsiasi punto all’interno di [0;1] e qualsiasi tipo di intervallo, avrai sempre lo stesso risultato.
Ciò invece non si può dire del punto x=2. Non essendo possibile disegnare degli intorni i cui punti ricadano nel dominio D, allora non è un punto di accumulazione e viene chiamato punto isolato.
Esempio 2
Dato il sottoinsieme A, verificare che x0 è un punto di accumulazione.
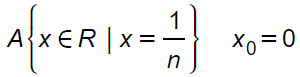
Svolgimento
Consideriamo per semplicità degli intorni sferici. Ad esempio sia I(0,ε) un intorno sferico di 0. Verifichiamo se viene rispettata la definizione di punto di accumulazione, cioè se tutti i suoi punti appartengono ad A.
Deve risultare che 1/n<ε. Cioè qualsiasi ε piccolo a piacere noi individuiamo ricadrà sempre in A. Se ad esempio:
ε=0.01, allora risulterà che ogni elemento 1/n, con n>1/ε=1/0,01=100 appartiene all’intorno scelto.
Ciò significa che la proprietà vale per ogni intorno di 0, per cui x0 è un punto di accumulazione.
Conclusioni
L’argomento generalmente a scuola non viene trattato in maniera molto approfondita. Tuttavia non è da trascurare perché è la premessa per la teoria dei limiti.
Un’ultima osservazione: il punto di accumulazione avrà anche una definizione non semplice da capire, ma alla fine si chiama “accumulazione” proprio perché all’interno vi si accumulano i punti.