I prodotti notevoli sono delle operazioni algebriche che permettono di velocizzare calcoli come moltiplicazioni e potenze di polinomi.
In buona sostanza si tratta di tante piccole “scorciatoie” che ci evitano di risolvere gli esercizi saltando numerosi passaggi. Ad esempio le moltiplicazioni tra polinomi possono risultare difficili e lunghe. Usando un semplice prodotto notevole si possono saltare numerosi passaggi per arrivare più agevolmente alla soluzione.
Di seguito trovi un formulario con tutti i prodotti notevoli che si studiano a scuola. Puoi cliccare sul nome di ciascuno per aprire la lezione guida di approfondimento.
1 – Prodotto di una somma per una differenza
La somma per la differenza di due binomi identici ma con un segno opposto si risolve elevando al quadrato il primo termine, meno il quadrato del secondo termine.
Il quadrato di binomio è pari al quadrato del primo termine più il doppio prodotto tra primo e secondo termine, più quadrato del secondo termine.
3 – Cubo di binomio
Il cubo del binomio è pari al cubo del primo termine, più il triplo prodotto del quadrato del primo termine per il secondo, più il triplo prodotto del primo per il quadrato del secondo, più il cubo del secondo termine.
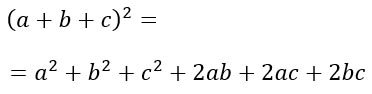
Il quadrato di trinomio è pari alla somma dei quadrati di tutti i termini, più il doppio prodotto del primo per il secondo, più il doppio prodotto del primo per il terzo, più il doppio prodotto del secondo per il terzo.
5 – Cubo di trinomio
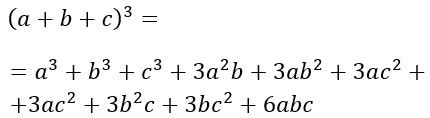
Il cubo di binomio è pari alla somma dei cubi dei tre termini, più tutti i tripli prodotti tra i termini con i rispettivi quadrati, più sei volte il prodotto dei tre termini. Ricordati che questo prodotto notevole, sviluppato, ha ben 10 termini.
6 – Somma di cubi
Questo tipo di prodotti notevoli viene utilizzato principalmente per le scomposizioni di polinomi, per cui nella maggior parte dei casi dovrai leggerlo da destra a sinistra.
La regola dice che la somma di polinomi è pari al prodotto del binomio somma per il trinomio composto da quadrato del primo, doppio prodotto negativo e quadrato del secondo.
Anche questi prodotti notevoli si applicano generalmente alle scomposizioni di polinomi.
La formula sottolinea che differenza di due cubi è pari al prodotto del binomio differenza tra i due termini per il quadrato del primo, il prodotto tra i due termini, più il quadrato del secondo termine.
8 – Potenze di polinomi
Abbiamo visto che le prime formule sui prodotti notevoli fanno riferimento al quadrato o al cubo. Cosa accade quando c’è una potenza di grado superiore? In tal caso si costruisce il Triangolo di Tartaglia con cui si individuano i coefficienti dei monomi.
9 – Trinomio speciale o trinomio caratteristico
Verrà molto usato anche come “scorciatoia” per risolvere le equazioni di secondo grado. In buona sostanza consiste nel trovare due numeri che sommati diano come risultato s e come prodotto p.
Per capire meglio perché queste formule sono così importanti, proviamo a fare un esempio e a risolvere assieme un semplice esercizio. Proviamo ad elevare al quadrato il seguente binomio:
Elevare al quadrato significa moltiplicare qualcosa per se stesso. Per cui possiamo anche scrivere:
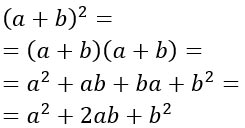
Come hai potuto osservare, nonostante l’esercizio sia semplicissimo, abbiamo impiegato 3 passaggi per arrivare alla soluzione. Utilizzando invece il secondo prodotto notevole visto sopra, si arriva alla soluzione in 1 solo passaggio. Immagina quanto questo possa essere comodo in esercizi più difficili o lunghi.
Cerchi espressioni o esercizi svolti? Vai agli esercizi sui prodotti notevoli
Di seguito trovi elencate gli ultimi appunti che riguardano i prodotti notevoli.