Alcuni studenti ci hanno scritto chiedendoci qualche chiarimento sulla regola della potenza di potenza. In questa lezione vedremo un approfondimento mirato con esempi ed esercizi svolti.
Come si calcola la potenza di una potenza? Come si risolvono quegli esercizi in cui la base è essa stessa una potenza?
Questa lezione viene in genere affrontata quando si parla delle proprietà delle potenze e capita spesso di incontrarla in esercitazioni o compiti in classe, per cui è importante saperla applicare bene. Ti renderai che è molto più semplice di quello che pensi.
Elevamento a potenza di potenza
La formula generale che puoi seguire è la seguente.
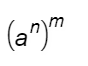
Si tratta quindi di una potenza che ha due esponenti, generalmente separati da una parentesi (può capitare anche che qualche testo la ometta). Ecco la regola da seguire così come la trovi sui libri di testo:
la potenza di potenza è una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti.
La definizione può sembrare difficile ma si tratta di un’operazione molto semplice. Quello che devi fare è:
- individuare la base e riscriverla: ti ricordi come fare? Ne abbiamo parlato in termini generali nella lezione sull’elevamento a potenza.
- individuare gli esponenti e moltiplicarli tra loro
Quindi il risultato che si ottiene è:
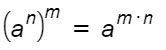
Potenza di potenza di potenza …
Molti studenti ci hanno chiesto: come fare quando invece ci sono più di due esponenti? Non cambia assolutamente nulla. Ti capiterà molto raramente, ma anche in tal caso basta semplicemente moltiplicarli tutti. Ecco la regola generale.
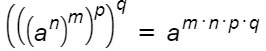
Anche avendo a che fare con più parentesi, la situazione come hai visto non è cambiata.
… abbiamo già finito!
Si, non c’è altro da sapere. La regola sulle potenze di potenze è davvero semplice, vediamo però ora con qualche esempio o caso particolare come si applica agli esercizi.
Esempi ed esercizi svolti
Potenza di potenza con parentesi
Vediamo di mettere in pratica quello che abbiamo appreso con un esempio semplicissimo. Proviamo a risolverlo assieme:
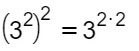
Come abbiamo fatto? Trascriviamo subito la base, cioè 3. Successivamente si moltiplicano i due esponenti (2 e 2). Il risultato è evidentemente 3 elevato a 4.
Potenza di potenza con esponente negativo
Abbiamo già parlato nelle precedenti lezioni di come si calcolano le potenze negative. In questo caso cerchiamo di evitare di porci inutili problemi e applichiamo solo la regola vista in questa lezione:
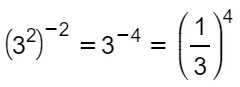
Nella prima parte non è cambiato nulla. Abbiamo fatto una moltiplicazione tra due numeri di segno opposto. Quindi (+2)×(-2) = -4.
A questo punto, non si tratta più di risolvere una potenza di una potenza, ma di un semplice esponente negativo. Per cui si invertono numeratore e denominatore e si lascia l’esponente togliendo il segno.
Potenza di potenza con base negativa
Che succede invece quando è la base ad avere il segno meno? Anche in questo caso applichiamo semplicemente la regola senza preoccuparci.
![]()
A questo punto poi, se l’esponente è pari, allora il segno meno andrà via, altrimenti si conserva. Nelle espressioni con sulle potenze, in genere, però non si fanno calcoli ulteriori e si lascia tutto così come abbiamo riportato.
Potenza di potenza con frazioni
Nel caso in cui la base sia una frazione non cambia assolutamente nulla rispetto al caso più banale visto nel primo esempio. Nel caso invece in cui ci siano degli esponenti con frazioni, allora si tratta di una semplice moltiplicazione di frazioni.
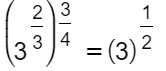
L’operazione banale da eseguire è 2/3 × 1/2 che dà come risultato 1/2.
Potenza di potenza elevata a zero
Sappiamo che qualsiasi numero elevato a 0 dà come risultato 1. Per questa ragione, anche quando ci sono le potenze di potenze, il risultato sarà sempre 1. Vediamo un esempio pratico.
![]()
Conclusioni
Abbiamo visto in questa lezione come si calcola la potenza di una potenza, andando ad analizzare i vari casi particolari che si possono incontrare negli esercizi.
Esiste in realtà anche una dimostrazione che spiega come si arriva alla formula di cui abbiamo discusso in questa lezione, ma generalmente non viene affrontata a lezione. Meglio attenersi sullo svolgimento degli esercizi.
Approfondimenti: esercizi ed espressioni con le potenze svolti e da svolgere