Isoperimetrici? Cosa vuol dire? Non lasciarti spaventare: il significato di questa parola è più semplice di quel che può sembrare! Dopo aver letto l’articolo ne sarai ancor più convinto!
Come si può fin da subito intuire, l’aggettivo isoperimetrico ha a che fare con il concetto di perimetro. Ricorderai che il perimetro di una figura geometrica è proprio il suo “contorno” e che viene calcolato sommando le lunghezze dei sui lati. Ricorderai inoltre che, in molti casi, il calcolo del perimetro può essere fatto servendosi di specifiche formule.
Isoperimetrici cosa vuol dire?
Si parla di figure isoperimetriche se e solo se i loro perimetri sono uguali.
NOTA: si parla di isoperimetria solo quando si ha a che fare con due o più poligoni. Per essere più chiari:
- Dire “Questo quadrato è isoperimetrico” è sbagliato!! Una figura geometrica ha la proprietà di essere isoperimetrica ad un’altra figura! Bisogna quindi specificare a cosa il poligono è isoperimetrico!
- Dire: “Questi due quadrati sono isoperimetrici” è corretto!
- Dire: “Questi tre quadrati sono isoperimetrici” è corretto!
- Ma è corretto anche dire: “Questo quadrato, questo triangolo e questo rettangolo sono isoperimetrici!”
Grazie a questi semplici esempi, si può capire come la proprietà di isoperimetria possa prendere in considerazione due o più poligoni e soprattutto due o più poligoni tra loro anche differenti. Non è importante che essi siano triangoli, rettangoli, quadrati, ecc.., l’importante è che abbiano lo stesso perimetro.
SUGGERIMENTO PER GLI ESERCIZI
Se, date due figure, ti viene chiesto di dire se sono isoperimetriche o meno, devi semplicemente calcolare il perimetro di entrambe e verificare che essi siano uguali cioè che abbiano lo stesso valore.
Esercizi svolti
Esercizio 1
Ecco dei semplici esempi che possono aiutarti a comprendere meglio quanto prima spiegato:
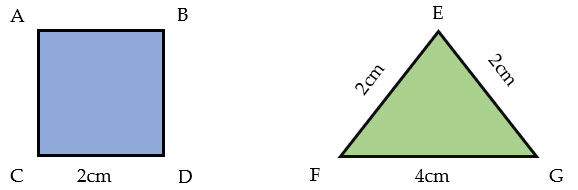
Per poter rispondere alla domanda è necessario come prima cosa calcolare i perimetri di entrambe le figure:
- Il perimetro del quadrato è dato dalla somma dei suoi lati ed è quindi pari a:
P(quadrato) = AB + BD + CD + CA = 2 cm + 2 cm + 2 cm + 2 cm = 8 cm
- Il perimetro del triangolo è dato dalla somma dei suoi lati ed è quindi pari a:
P(triangolo) = EG + GF + FE = 2 cm + 2 cm + 4 cm = 8 cm
Ora puoi verificare che i due valori calcolati siano uguali e affermare che quadrato e rettangolo sono isoperimetrici.
Considerazioni:
- Ricorda che per poter calcolare il perimetro di una figura geometrica puoi utilizzare anche le formule. In questo specifico caso, il perimetro del quadrato può essere calcolato moltiplicando per 4 la lunghezza di un suo lato.
- L’unità di misura utilizzata per indicare le lunghezze è del tutto arbitraria. Possono essere centimetri (cm), metri (m) o anche semplicemente unità.
- Il perimetro di una figura geometrica molto spesso è indicato con 2P piuttosto che con P. Si tratta semplicemente di una scelta sulla simbologia da adottare!
Esercizio 2
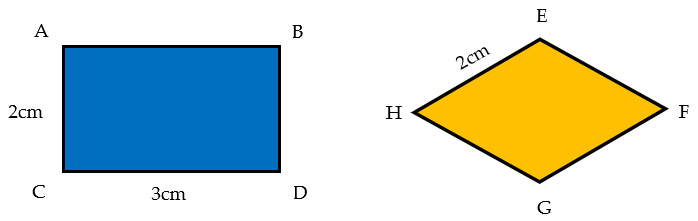
Rombo e rettangolo sono isoperimetrici? Per poter rispondere alla domanda, il procedimento è sempre lo stesso:
- Calcoliamo il perimetro del rettangolo:
P(rettangolo)= 2 × AB + 2 × BD = 2 × 3cm + 2 × 2cm = 6cm + 4 cm = 10cm - Calcoliamo il perimetro del rombo:
P(rombo) = 4 × EF = 4 × 2cm = 8cm - Verifichiamo che i perimetri abbiano lo stesso valore. In tal caso le misure non corrispondono per cui i due poligoni non sono isoperimetrici.
In questo esempio è stato seguito lo stesso procedimento usato nell’esercizio precedente. Il perimetro delle figure è stato calcolato utilizzando la rispettiva formula. Vedi perimetro rettangolo e/o perimetro rombo nel caso in cui avessi dubbi!
Esercizio 3
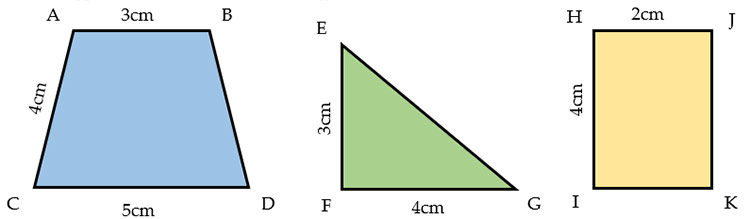
- Calcoliamo il perimetro del trapezio isoscele:
P(trapezio) = 2 x AC + AB + CD = 2 x 4cm + 3cm + 5cm = 16cm
- Calcoliamo il perimetro del triangolo rettangolo. Esso è dato dalla somma dei suoi 3 lati. Come puoi notare dalla figura vengono forniti solo i due valori dei due cateti (FE e GF). Come possiamo trovare il calcolo dell’ipotenusa?
Anche in questo caso non c’è niente di cui preoccuparsi: si può utilizzare il Teorema di Pitagora.
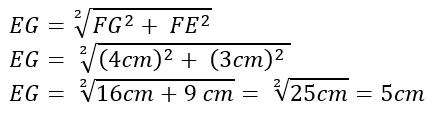
A questo punto possiamo calcolare la somma dei tre lati:
P(triangolo) = EG + FG + FE = 5cm + 4cm + 3cm = 12cm
- Calcoliamo il perimetro del rettangolo:
P(rettangolo) = 2 x HJ + 2 x HI = 2 x 2cm + 2 x 4cm = 12cm
Arrivati a questo punto possiamo confrontare i valori trovati per accorgerci che il trapezio e il triangolo non sono isoperimetrici, così come il trapezio e il rettangolo. Rettangolo e triangolo sono invece isoperimetrici.
Poligono equiestesi e isoperimetrici
L’isoperimetria non è l’unica proprietà geometrica che due o più poligoni possono avere. Molto spesso essa viene confusa con l’equivalenza o con la congruenza. Per questo motivo è bene sottolineare le differenze:
- due poligoni sono isoperimetrici se hanno lo stesso perimetro;
- due poligoni sono equivalenti se hanno la stessa area;
- due poligoni sono congruenti se sovrapposti, coincidono;
Ti starai chiedendo: ma due poligoni che hanno la stessa area, hanno anche lo stesso perimetro? Oppure, due poligoni che hanno lo stesso perimetro hanno anche la stessa area? Più in generale: che relazioni esistono tra le tre proprietà?
Due poligoni isoperimetrici sono anche equivalenti?
Innanzitutto è bene chiarire che due figure isoperimetriche non sono necessariamente equivalenti. Sono due concetti differenti: uno riguarda il perimetro, l’altro riguarda l’area! In altre parole, la risposta alla domanda: due poligoni che hanno la stessa area, hanno anche lo stesso perimetro? E viceversa, è: dipende!
Per poter rispondere bisogna:
- calcolare il perimetro di entrambe le figure;
- confrontare i due valori trovati, se uguali allora le figure sono isoperimetriche;
- calcolare l’area di entrambe le figure;
- confrontare i due valori trovati, se uguali allora le figure sono equivalenti.
Questo è il metodo più semplice di procedere. Ci sono alcuni casi particolarmente semplici, ad esempio se vengono confrontati due quadrati, che sono due poligoni regolari. Questi se sono equiestesi sono anche isoperimetrici.
Isoperimetria e congruenza
Se due figure sono congruenti allora sovrapposte coincidono. Se coincidono vuol dire che hanno lo stesso perimetro e la stessa area. Possiamo quindi affermare che:
- due poligoni congruenti sono sempre isoperimetrici
- due poligoni congruenti sono sempre equivalenti
Attenzione!!! L’implicazione inversa non è sempre vera!!! In altre parole è sbagliato dire che due poligoni isoperimetrici sono congruenti.
CONCLUSIONE
Abbiamo visto che per poter dire se due figure geometriche sono isoperimetriche o meno basta confrontare i loro perimetri. Per farlo è necessario calcolarli esplicitamente, spesso è necessario utilizzare formule specifiche che puoi trovare su un qualsiasi formulario! Come hai visto nei vari esempi, i passi da seguire sono sempre gli stessi.
Ricorda di tener presente la differenza tra isoperimetria, equivalenza e congruenza!
Se l’articolo è stato utile e di tuo gradimento, lascia un commento!!!