Piano cartesiano: definizione e spiegazione completa

Il piano cartesiano è il sistema di riferimento utilizzato in geometria analitica per disegnare le figure geometriche sia piane che solide. Si compone di due assi cartesiani ortogonali che consentono l’individuazione precisa (e univoca, cioè senza possibilità di errore) di un punto.

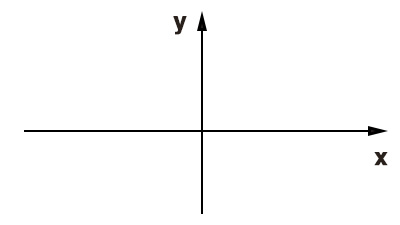
I due assi del riferimento cartesiano indicate con x e y, si chiamano rispettivamente asse delle ascisse e asse delle ordinate. Dall’intersezione di ogni “linea cartesiana” si ricava un punto – generalmente indicato con la lettere O – chiamato origine del piano cartesiano.

Le due rette dividono il piano di riferimento cartesiano in 4 aree che vengono definite quadranti. Ci sono quindi 4 quadranti e per convenzione si dice che il primo quadrante è quello in alto a destra. Poi si procede il senso antiorario: il secondo è in alto a sinistra, il terzo in basso a sinistra e il quarto in basso a destra.

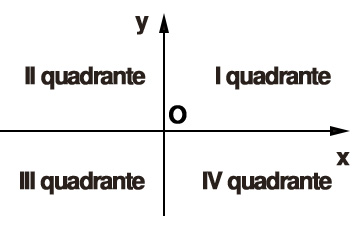
Perché si chiama piano cartesiano?

L’uso delle coordinate venne introdotto nella prima volta nel XIV secolo, ma fu solo grazie al matematico René Descartes (italianizzato Cartesio) che la teoria che sta alla base della geometria analitica venne elaborata in maniera più precisa e organica.

Piano cartesiano spiegazione

Il sistema di riferimento cartesiano viene chiamato spesso anche OXY, riprendendo le tre componenti principali: origine, ascisse e ordinate.

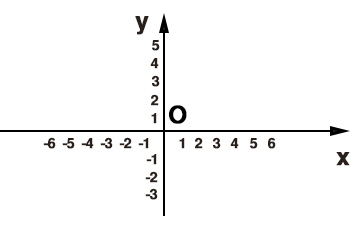
Per poterne dare una spiegazione ancora più semplice, immagina il piano cartesiano come un foglio di lavoro. A partire dall’origine è possibile andare a numerare sia l’asse delle x che delle y che, quindi, sono delle rette orientate. Questo vuol dire che a partire da O, andando verso il verso della freccia (procedendo a destra le x o in alto le y) il valore aumenta. In senso opposto il valore diminuisce.

Dal piano cartesiano al punto

In questo modo un generico punto si può sempre individuare assegnandogli una coppia di valori: una x e una y. Un po’ come si fa nella battaglia navale!

Il punto generico si indica con le parentesi tonde P(x,y). Ad esempio il punto di coordinate A(3;2) ha ascissa 3 e ordinata 2. Lo andiamo a individuare sul grafico e si ottiene il seguente disegno:

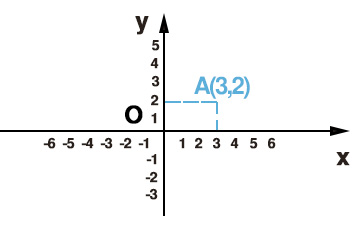
SPIEGAZIONE PASSO PASSO: Come abbiamo fatto? Dall’asse delle x abbiamo preso il valore 3 e abbiamo tracciato la proiezione ortogonale (la linea verticale tratteggiata in blu). Dall’asse delle y abbiamo preso il valore 2 e tracciato la proiezione ortogonale (la linea orizzontale tratteggiata in blu). Dall’intersezione delle due proiezioni, si è ottenuto il punto A di coordinate quindi 3 e 2.

Dal punto alla retta

Come è noto dalla geometria euclidea che si studia anche alle scuole medie, per poter disegnare tutte le figure abbiamo bisogno di 3 enti geometrici fondamentali: punto, retta e piano.

Il piano cartesiano è il foglio di lavoro, il punto lo abbiamo individuato. Come fare per la retta? Vedremo nelle prossime lezioni in maniera più dettagliata come affrontare la retta nel piano cartesiano. Per ora ci basti sapere che – usando la definizione classica – la retta non è altro che un insieme infinito di punti allineati. Dalla retta poi potremo individuare superfici di lavoro e quindi porzioni di piano.

Come potrai vedere nelle prossime lezioni, in geometria analitica potremo disegnare un triangolo, una circonferenza, una parabola e tante altre figure geometriche.

Il piano cartesiano tridimensionale

Quello che abbiamo visto fino ad ora è un sistema di riferimento bidimensionale. Proprio come se fosse un foglio di lavoro, il piano cartesiano OXY ti consente di disegnare solo figure in 2D.

Proseguendo con gli studi di matematica, più in avanti, avrai la possibilità di verificare che esiste anche un riferimento tridimensionale, composto dagli assi x, y, e z. In questo modo potrai anche disegnare e studiare figure 3D.

Conclusioni

La lezione sul piano di riferimento cartesiano si conclude. Sei pronto per passare alle prossime lezioni sul punto, sulla retta e sulle prime formule, come il calcolo del punto medio di un segmento o la distanza punto-retta.

Se la spiegazione di oggi ti è stata utile e l’hai trovata chiara, lasciaci un commento in basso. Ci aiuterai a migliorare ogni giorno la qualità delle lezioni e a offrirti sempre più contenuti per aiutarti con il tuo programma di matematica.