L‘ortocentro del triangolo è il punto di intersezione delle tre altezze. In questa lezione vediamo come si disegna, quali sono le sue proprietà e soprattutto come varia questo punto particolare nei vari tipi di triangoli.
Per capire che cos’è l’ortocentro di un triangolo, è indispensabile sapere come si disegna e che cos’è l’altezza relativa ad ogni lato. Ricordiamo che l’altezza si definisce come il segmento che parte da un vertice e cade perpendicolarmente sul lato opposto.
Ortocentro definizione
L’ortocentro di un triangolo è il punto di incontro delle altezze relative ai tre lati. Per poterlo disegnare, dato un triangolo scaleno ABC, disegniamo le tre altezze, cioè le perpendicolari dai tre vertici.
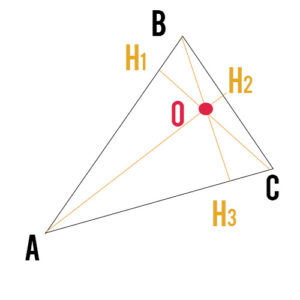
Dall’intersezione delle tre altezze si ottiene il punto O, detto ortocentro del triangolo. Come puoi vedere dalla figura, in un triangolo acutangolo questo punto caratteristico cade all’interno della figura.
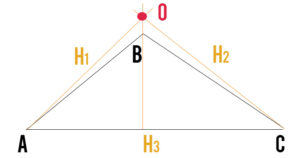
Nell’ultima figura puoi notare come l’ortocentro del triangolo ottusangolo ABC (ottuso in B) sia esterno alla figura. Puoi provare a ripetere il disegno e vedrai che maggiore è l’angolo e più il punto è esterno.
Caratteristiche e proprietà
- L’ortocentro del triangolo rettangolo coincide proprio con il vertice corrispondente all’angolo retto.
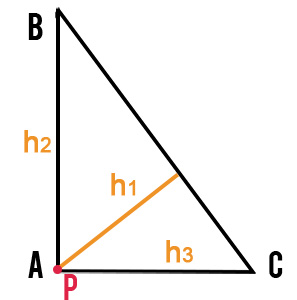
- L’ortocentro del triangolo isoscele è allineato con baricentro e circocentro su quella che viene chiamata retta di Eulero.
- L’ortocentro del triangolo equilatero coincide con il baricentro e il circocentro.
La formula per calcolare l’ortocentro in geometria analitica
Esistono due metodi per trovare questo particolare punto per qualsiasi tipo di triangolo. Il primo è sicuramente quello più istantaneo e semplicemente sfrutta una formula:
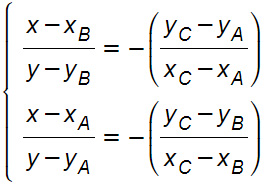
dove A, B, C sono i tre vertici del triangolo. In questo sistema di equazioni le incognite da individuare sono x e y, ovvero ascissa e ordinata dell’ortocentro del triangolo.
Il secondo metodo è invece per chi non ricorda la formula a memoria. Date le coordinate tre vertici:
- si calcolano le rette corrispondenti ai lati AB, AC e BC.
- Si calcola la retta corrispondente all’altezza relativa ad AB. Per cui si trova una retta passante per un puntoe coefficiente angolare anti-reciproco a quello di AB.
- Stessa cosa per l’altezza relativa ad AC.
- Si costruisce un sistema con due equazioni: al primo rigo c’è la retta altezza 1, al secondo rigo c’è la retta altezza 2. Dalla soluzione di questo sistema si ottengono le coordinate dell’ortocentro.
Conclusioni
L’ortocentro dei triangoli è un ente geometrico che non si incontra molto spesso durante il programma i geometria euclidea o analitica. Tuttavia si tratta di un utile approfondimento per capire meglio i punti caratteristici dei triangoli.
Se la lezione è stata di tuo gradimento e l’hai trovata utile, oppure se hai ancora dubbi o hai bisogno di chiarimenti, lascia un commento alla fine di questo articolo. Il nostro staff ti risponderà nel minor tempo possibile.
mi siete stati molto d’aiuto, grazie<3
spero che chi sta leggendo stia avendo una buona giornata, chiunque tu sia ti voglio bene e sei perfetta/o così come sei, non farti mai abbattere da nessuno e da alcuna situazione che la vita ti pone davanti. so che riuscirai a raggiungere tutti i tuoi obbiettivi se ci metti davvero amore e dai il 100% di te stesso. ricorda di pensare positivo, la positività attrae cose positive all'interno della tua vita, se fai prendere il sopravvento alla tua visione negativa vedrai solo il lato peggiore delle cose, conducendo te stesso all'interno di un ciclo continuo. <3
ps: ricorda di mantenerti idratato bevendo acqua