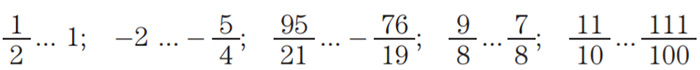I numeri razionali sono quei numeri che possono essere espressi attraverso una frazione di un numeratore su un denominatore. In matematica l’insieme dei numeri razionali viene indicato con la lettera Q ed ha un numero infinito di elementi.
Ci hai capito poco? Non preoccuparti, in questa lezione vedremo quali sono i numeri razionali, quali sono le differenze con gli altri insiemi numerici e che caratteristiche hanno.
Perché esistono i numeri razionali?
Nell’insieme dei numeri naturali N e dei numeri relativi Z non sempre è possibile eseguire una divisione. Se provi a svolgere 7:2 ottieni un numero non intero, cioè 3,5.
Per poter sempre fare la divisione, è necessario ampliare l’insieme dei numeri interi relativi aggiungendo quelli che sono definiti come numeri razionali.
Che utilità hanno nella vita reale? Ecco un esempio concreto: “oggi mezza classe era assente”. Quella parola mezza indica la divisione 1:2 che non ha un risultato intero.
Numeri razionali – definizione
Oltre alla definizione che abbiamo dato all’inizio di questa lezione, possiamo anche dire che l’insieme dei numeri razionali Q è dato da tutti i numeri che possono essere espressi sotto forma di frazione.
Ti ricordi che cos’è una frazione? E’ un’operazione matematica (identica alla divisione) in cui, dati due numeri a e b, si ha:
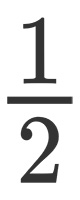
Tutto ciò che si trova al di sopra della linea di frazione si chiama numeratore. Ciò che si trova al di sotto della linea di frazione si chiama denominatore.
Si fa notare come i numeri interi e i numeri relativi siano un sottoinsieme dei numeri razionali. Questo perché anche un numero intero può essere espresso come una frazione con al denominatore 1.
Ad esempio il numero intero 23, può anche essere riscritto come la frazione 23/1.
Differenza tra numeri razionali e irrazionali
I numeri irrazionali sono dei numeri che appartengono sempre all’insieme dei numeri reali, ma non sono razionali. Mentre questi possono essere espressi attraverso la frazione i due numeri, gli irrazionali sono quei numeri la cui espansione non termina mai e non forma mai una sequenza periodica.
Ad esempio:
- 2/3 = 0,6666…… NON E’ UN NUMERO IRRAZIONALE
- √2 = 1,414213562…. E’ UN NUMERO IRRAZIONALE
Numeri razionali a confronto – qual è il più grande?
Non è semplice giudicare, tra due frazioni, quale delle due mi dia come risultato il numero razionale maggiore. Esistono tuttavia alcune tecniche che rendono il confronto tra due numeri razionali molto semplice e veloce:
- Se due numeri razionali hanno stesso numeratore e stesso denominatore allora sono uguali.
- Se due numeri razionali hanno stesso denominatore, allora sarà maggiore il numero con il numeratore maggiore.
Esempio: 7/6 è maggiore di 5/6 - Se due numeri razionali hanno stesso numeratore, allora sarà maggiore il numero con il denominatore minore.
Esempio: 7/4 è maggiore di 7/5 - Se due numeri hanno numeratore e denominatori diversi, allora bisogna trasformare le frazioni in modo che abbiano lo stesso denominatore. Si calcola quindi il minimo comune multiplo.
Esempio:
Date le due frazioni 3/4 e 4/5, quale delle due è maggiori?
Dobbiamo innanzitutto calcolare il mcm tra 4 e 5, che è pari a 20. A questo punto trasformiamo entrambe le frazioni, dividendo il mcm per il denominatore e moltiplichiamo il risultato per il numeratore.
3/4 → Al denominatore ho quindi il mcm 20 e al numeratore ho 20 diviso 4 per 3 → 15/20
4/5 → Al denominatore ho sempre il mcm 20 e al numeratore ho 20 di 5 per 4 → 16/20
A questo punto in base alla prima regola vista sul confronto tra numeri razionali, ho che 3/4 è minore di 4/5.
Esercizi sui numeri razionali
Esercizio 1
In base a quello che abbiamo studiato in questa lezione, prova a rispondere alle seguenti domande.
- che cos’è un numero razionale?
- esiste un numero razionale uguale al suo opposto? Qual è?
- perché il concetto di “successivo” nei numeri razionali non ha senso? (ricordati che i numeri razionali sono infiniti)
Se non sei stato in grado di rispondere ad una delle domande sopra, scrivici nei commenti 😉
Esercizio 2
Inserisci il simbolo < (minore) o > (maggiore) al posto dei puntini.