Categoria: Triangoli
I triangoli sono figure geometriche costituiti da 3 lati. Sono i poligoni con il minor numero di lati, visto che non ne esistono formati da 2 lati.
ELEMENTI DEL TRIANGOLO
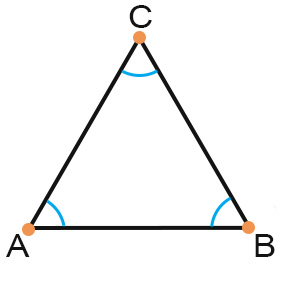
Un triangolo è composto da:
- tre lati – disegnati in nero e che indichiamo con AB, BC e AC;
- tre angoli – disegnati in blu, in A, in B e in C;
- tre vertici – disegnati in arancione, nei punto A, B e C
Classificazione dei triangoli
In base al rapporto tra i lati o tra gli angoli possiamo distinguere diversi tipi di triangoli che per possiamo inserire in questa semplice tabella:
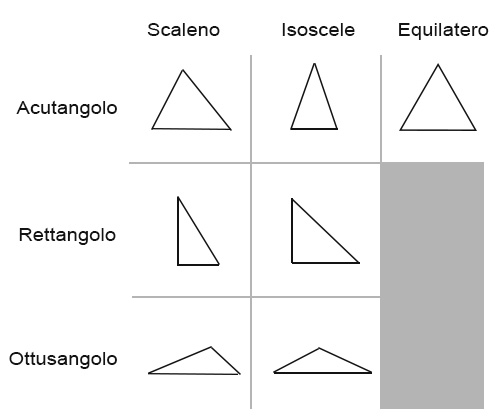
In base al rapporto tra i lati si definisce:
- triangolo scaleno – ha la caratteristica di avere tutti i lati differenti;
- triangolo isoscele – ci sono due angoli e due lati congruenti;
- triangolo equilatero – ci sono tutti lati e angoli congruenti;
In base al rapporto tra gli angoli si definisce:
- triangolo acutangolo – ha tutti gli angoli acuti, cioè minori di 90°;
- triangolo rettangolo – ha un angolo retto, cioè di 90°;
- triangolo ottusangolo – ha un angolo ottuso, cioè maggiore di 90°
Triangoli formule
Quali sono le formule del triangolo? Cerchiamo di riassumere le principali e le più semplici ed immediate utilizzate in problemi ed esercizi. Dato il triangolo ABC:
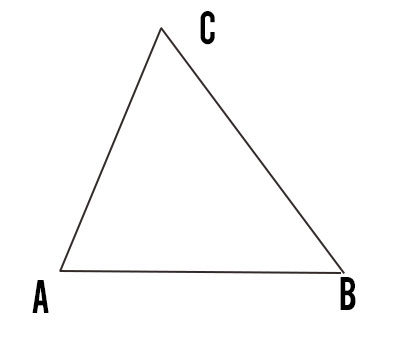
Perimetro
Il perimetro, per qualsiasi tipo di triangolo, è sempre pari alla somma dei tre lati. Per cui possiamo scrivere la seguente formula:
![]()
Area
Sempre in riferimento ad un triangolo scaleno generico, l’area si può calcolare con la formula classica imparata alle scuole elementari: base per altezza diviso due.
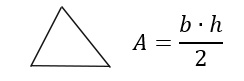
Approfondimenti: come calcolare l’area del triangolo scaleno
Nel caso di triangoli particolari la formula si può semplificare.
Triangolo rettangolo: poiché uno dei due cateti coincide con l’altezza, allora l’area si può calcolare come semiprodotto dei cateti.
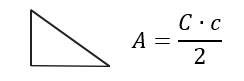
Approfondimenti: calcolo area del triangolo rettangolo
Triangolo equilatero: considerando che tutti i lati L sono uguali e che su di essi si può applicare il teorema di Pitagora, allora la formula dell’area può essere anche calcolata come:
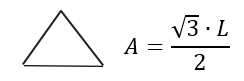
Approfondimenti: calcolo dell’area del triangolo equilatero
Punti notevoli dei triangoli
Diamo di seguito alcuni riferimenti che potrai andare ad approfondire sui vari link. Iniziamo proprio dal segmento più importante: l’altezza.
- Per definizione, l’altezza di un triangolo è il segmento che congiunge un qualsiasi vertice con il lato opposto. L’intersezione delle tre altezze chiama ortocentro (O).
- La mediana, invece, è il segmento che unisce un qualsiasi vertice con il punto medio del lato opposto. L’intersezione delle tre mediane si chiama baricentro (G).
- La bisettrice è il segmento che ha estremi nel vertice e nel lato opposto, dividendo a metà l’angolo. L’intersezione delle tre bisettrici si chiama incentro (I).
- L’asse è il segmento che cade perpendicolarmente su un lato dividendolo esattamente a metà. L’intersezione dei tre assi si definisce circocentro (C).
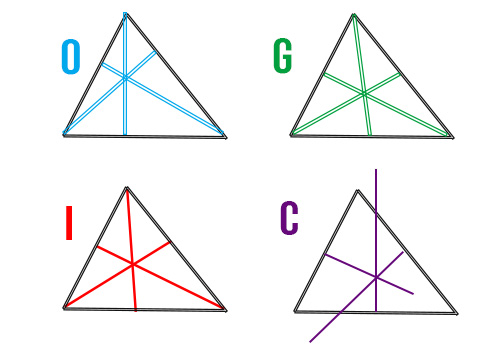
Proprietà dei triangoli
- Poiché per tre punti non allineati passa sempre una sola circonferenza, vuol dire che il triangolo può essere sempre circoscritto o inscritto ad una circonferenza.
- La somma degli angoli interni di un triangolo è 180°.
- La somma di due lati è sempre minore al terzo lato e la differenza tra due lati è sempre maggiore al terzo lato.