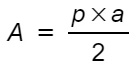Categoria: Esagono

L’esagono è un poligono formato da 6 lati e 6 angoli. Si parla di esagono regolare quando questa stessa figura geometrica ha i 6 lati (e quindi anche gli angoli) tutti uguali.

In questa questa pagina trovi una lezione generale che riguarda l’esagono regolare, dalle formule utilizzate alla definizione sino ad alcuni riferimenti sulla costruzione. Alla fine dell’articolo trovi invece tutti gli approfondimenti mirati e gli esercizi svolti.

Che cos’è un esagono

Prima di dare una definizione rigorosa, cerchiamo di capire da dove deriva questa parola. In questo modo ci sarà tutto più chiaro.

Significato ed etimologia

Si tratta di una parola composta che deriva dal greco, formata da:

• esa: exi, che significa letteralmente sei;
• gono: gonia che signifia letteralmente angolo.

Definizione

Da quanto appena appreso possiamo dire che l’esagono è il poligono formato da 6 angoli. Sui libri di testo si legge, in alternativa, che l’esagono è per definizione la figura geometrica composta da 6 lati.

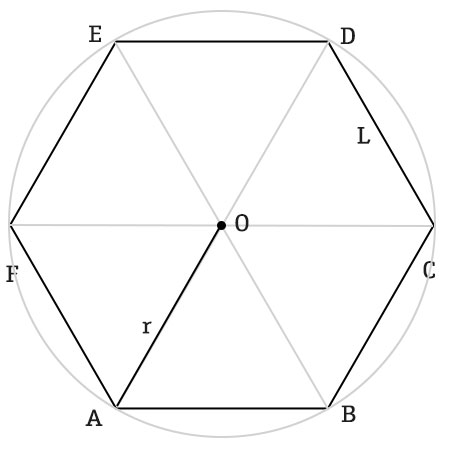
Proprietà dell’esagono

Come puoi notare dalla figura, tracciando le diagonali, si generano tanti triangoli isosceli. Tra poco dimostreremo che si può fare un’ulteriore precisazione.

L’angolo in O, al centro della figura, può essere suddiviso in 6 angoli. Ciascuno di questi è ampio 360°:6=60°. Sapendo che la somma degli angoli interni di un triangolo è 180°C, allora ciascuno degli angoli alla base vale (180°-60°):2 = 60°. Questo significa che gli angoli sono tutti uguali. Arriviamo così alla prima proprietà.

• I 6 triangoli formati dalle diagonali dell’esagono hanno tutti i lati e gli angoli uguali, per cui sono triangoli equilateri.
• Ogni vertice dell’esagono è formato da un angolo di ampiezza 120°.
• In tutto la figura ha 9 diagonali (prova a disegnare anche quelle non corrispondenti)
• Il punto O, intersezione delle diagonali, è anche il centro della circonferenza inscritta e circoscritta.
• La somma degli angoli interni dell’esagono è (n-2)·180° = (6-2)·180° =720°
• Il centro dell’esagono è anche asse di simmetria.

Esagono formule

Il formulario che stiamo per presentarti è praticamente identico alle altre figure geometriche regolari che abbiamo trattato in altre lezioni.

Per cui premettiamo che esistono due costanti utili ai fini del calcolo e che trovi tabellate in tutti i libri di testo di matematica. Iniziamo proprio dalla loro definizione.

Numero fisso e apotema

E’ un numero grazie al quale si può calcolare l’apotema dell’esagono partendo dalla misura del lato.

f=0,866

Per calcolare l’apotema basta moltiplicare il lato per 0,866.

a=L · f

Costante d’area

E’ quel numero tabellato che permette di calcolare l’area dell’esagono noto il lato. Si indica con la lettera greca φ (si legge fi).

φ = 2,598

Area esagono

• Dato il lato – Per calcolare la superficie è sufficiente moltiplicare la costante d’area per il lato al quadrato.

A=φ · L²

• Dato l’apotema e il perimetro – formula meno usata ma che è riportata su molti libri di testo. L’area si calcola moltiplicando il semiperimetro per l’apotema.

Perimetro esagono

Essendo una figura geometrica regolare, è sufficiente moltiplicare la misura del lato per il numero di lati. Per cui possiamo scrivere:

p= 6 · L

Sfruttando le formule inverse di quelle viste sino ad ora possiamo determinare la misura dell’apotema, del lato o del perimetro partendo dall’area.

Esercizio svolto

Calcolare perimetro e area di un esagono regolare  con lato pari a 10 cm.

Svolgimento

Iniziamo subito calcolando il perimetro.

P=6L=60 cm

Per quanto riguarda l’area, invece, sfruttiamo la costante φ:

A=φ · L² = 2,598 · 100 = 259,8 cm²