Il concetto di funzioni pari e dispari compare nello studio di funzione quando si va studiare la presenza di simmetrie nel grafico. Iniziamo subito con le definizioni generali.
Funzione pari: una funzione si dice pari quando f(x)=f(-x) e graficamente presenta una simmetria rispetto all’asse delle ordinate.
Funzione dispari: una funzione si dice dispari quando f(x)=-f(-x) e graficamente presenta una simmetria rispetto all’origine.
Vediamo di essere ora più chiari e cerchiamo di capire anche graficamente cosa vuol dire studiare una funzione pari o dispari.
Funzioni pari
La caratteristica della funzione pari è di rispettare la proprietà:
f(x) = f(-x)
Cosa significa? Che puoi riscrivere la funzione assegnata inserendo, al posto della x, una parentesi con (-x). Anche facendo questa piccola modifica si ritornerà di nuovo alla traccia iniziale.
Vediamo con un semplice esempio.
Verificare che y=x^2 che una funzione pari o dispari.
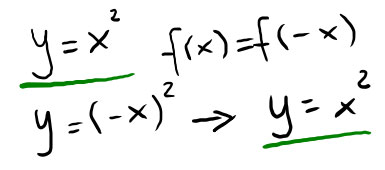
Semplicemente al posto della x abbiamo inserito (-x). Sviluppando il quadrato ci siamo ricondotti esattamente al punto di partenza. Abbiamo così dimostrato che la funzione è pari.
Grafico delle funzioni pari
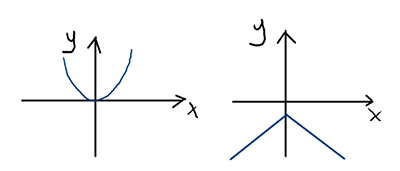
Dal punto di vista grafico, la presenza di funzioni pari o dispari va ad agevolarci notevolmente lo studio di funzione. Una funzione pari infatti presenta una simmetria rispetto all’asse y.
Senza entrare troppo nei dettagli riguardanti le trasformazioni geometriche, si ricorda che la simmetria rispetto all’asse delle ordinate è tale per cui vale la formula:
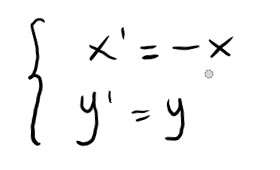
Funzioni dispari
La caratteristica delle funzioni dispari è di rispettare la proprietà:
f(x) = – f(-x)
Cosa significa? Che puoi ripetere il procedimento visto prima, quindi sostituire (-x) al posto della x, ricordandoti di aggiungere un segno meno a tutta la funzione. Vediamo con un esempio.
Verificare che la funzione y=x^3 sia una funzione pari o dispari.
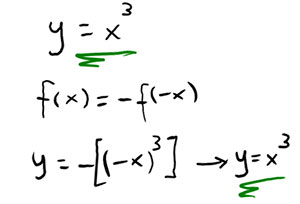
Come puoi notare nell’esempio, andando a mettere un segno meno davanti alla funzione e sostituendo (-x) al posto della x, ci siamo ricondotti esattamente al risultato di partenza. Abbiamo così dimostrato che y=x^3 è una funzione dispari.
Grafico delle funzioni dispari
Dal punto di vista grafico una funzione dispari si caratterizza per una simmetria rispetto all’origine, come nei due esempi in figura.
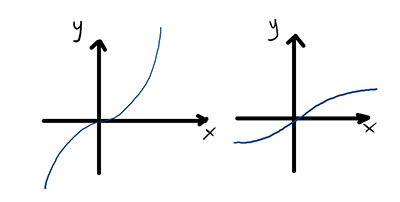
Si ricorda che la simmetria rispetto all’origine viene espressa dalla trasformazione geometrica:
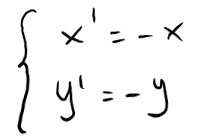
Domanda per gli studenti
In base a quello che hai letto fino ad ora, possono esistere funzioni pari e dispari simultaneamente? Scrivici nei commenti la tua opinione.
Esempi ed esercizi
Verifiche che se le seguenti funzioni siano da funzioni pari o dispari.
Esercizio 1
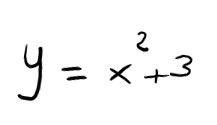
Iniziamo con la verifiche necessaria per le funzioni pari. Sostituiamo quindi (-x) al posto di x.
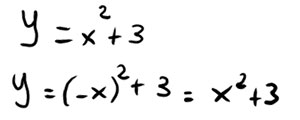
Si nota come il risultato finale sia uguale alla traccia iniziale. Per questa ragione possiamo indicare che la funzione è PARI.
Esercizio 2
Verificare che y=senx sia una funzione pari o dispari.
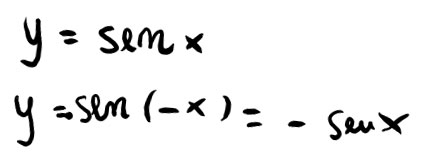
Abbiamo subito provato a sostituire (-x) al posto di x per studiare la prima simmetria, che non è verificata. Quindi la funzione non è pari.
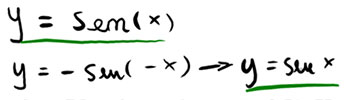
Andando ad aggiungere un segno meno davanti la funzione iniziale (oltre che sostituire -x al posto di x) si torna alla funzione di partenza. Per questa ragione y=senx è una funzione PARI.
Esercizio 3
Verificare che y=1/x sia una funzione pari o dispari.
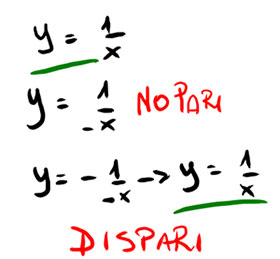
Abbiamo ripetuto tutti i calcoli visti fino a questo momento. Per dimostrare che è una funzione pari abbiamo sostituito (-x) al posto di x e la condizione non è verificata.
Aggiungendo anche il segno meno all’esterno della funzione, la condizione è verificata per cui la funzione è DISPARI.
MA ATTENZIONE! La funzione è dispari solo nel dominio. Poiché per x=0 la funzione non esiste (vedi Dominio di una funzione – come si calcola il campo di esistenza), allora la funzione è sempre dispari tranne che a 0. Per cui possiamo scrivere:
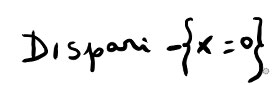
Esercizio 4
Il coseno iperbolico è una funzione pari o dispari? Studiamo subito la funzione:
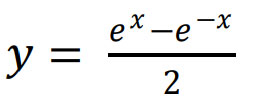
Iniziamo subito con la definizione di funzione pari: f(x)=f(-x)
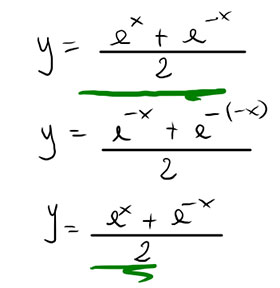
Esercizio 5
La traccia è identica all’esercizio precedente. Stabilire se si tratta di una funzione pari o dispari.
y=(x+3)^2
Cominciamo come sempre dalla condizione di funzione pari f(x)=f(-x)
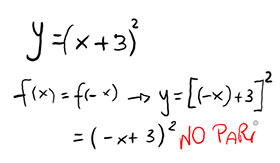
Poiché la condizione non è soddisfatta, proviamo a verificare che si tratti di una funzione dispari con f(x)=-f(-x).
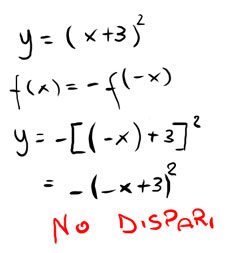
In questo particolare esempio, notiamo che la funzione non è né pari né dispari, per cui non abbiamo nessun tipo di simmetria del grafico.
Conclusioni
Abbiamo visto in questa lezione che determinare se una funzione è pari o dispari è estremamente semplice e generalmente richiede pochi semplici passaggi.
Se questa lezione ti è stata utile, ti chiediamo di lasciare un commento sotto. La tua opinione è importante per correggere errori e per migliorarci ogni giorno e fornirvi sempre contenuti gratis e di qualità.
molto utile! bravi!