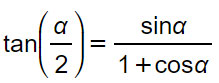Le formule di bisezione del seno, coseno e tangente consentono di mettere in relazione un angolo (alfa, α) con la sua metà (alfa mezzi, α/2).
Si ricavano a partire dalle formule di duplicazione e vengono spesso utilizzate per risolvere gli esercizi sulle equazioni goniometriche. Iniziamo però vedendo quali sono le formule di bisezione in questo piccola tabella.
Formule di bisezione
Formula di bisezione del seno
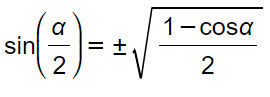
Formula di bisezione del coseno
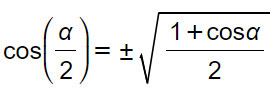
Formula di bisezione della tangente
oppure
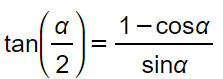
ATTENZIONE: La formula di bisezione tangente è valida solo se viene soddisfatta la condizione di esistenza (denominatore diverso da 0). Cioè:
- 1+cosα≠0 → α≠180°+kπ
- sinα≠0 → α≠kπ
Esempi svolti
Determiniamo le funzioni goniometriche di 22,5°.
L’angolo su cui ci viene chiesto di eseguire uno studio è la metà dell’angolo di 45°. Per questa ragione possiamo calcolare seno, coseno e tangente di 45°/2.
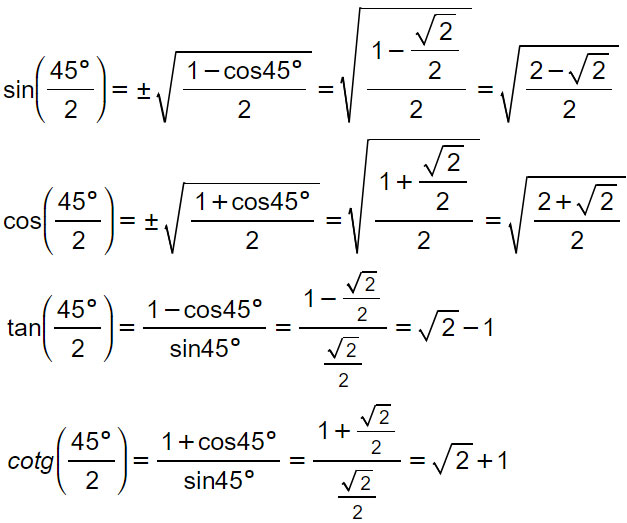
Dimostrazione formule bisezione seno e coseno
Bisezione del coseno dimostrazione
Si parte dalla formula di duplicazione del coseno:
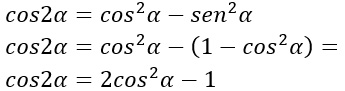
A questo punto andiamo ad effettuare una sostituzione. Introduciamo una nuova variabile che chiamiamo x=2a. In questo modo otteniamo delle nuove formule:
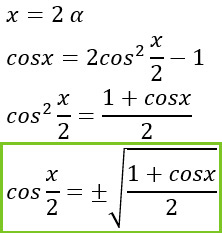
Per verificare la formula del seno, ci riscriviamo la formula di duplicazione vista prima in funzione del seno.

Formula bisezione tangente e cotangente
Trovate le formule di bisezione seno e coseno, basta sfruttare le relazioni fondamentali della trigonometria per andare avanti con le dimostrazioni. Sappiamo infatti che la tangente di un angolo è il rapporto tra seno e coseno, per cui possiamo scrivere:
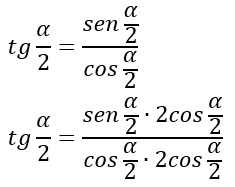
Abbiamo moltiplicato per 2 per coseno di alfa mezzi a numeratore e denominatore. Sopra possiamo applicare la formula di duplicazione del seno (2senxcosx=sen2x) e sotto semplicemente svolgiamo la formula.
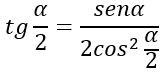
Al denominatore applichiamo la formula di bisezione del coseno che abbiamo ricavato precedentemente:

Per la cotangente basta semplicemente invertire numeratore e denominatore visto che cotgx=1/tgx.
Formule bisezione, esercizi svolti
In questo ultimo paragrafo vedremo come si usano le formule di bisezione con degli esempi pratici con cui provare le formule appena calcolate.
Esercizio 1
Calcolare la tangente di 45°/2.
Si fa presente che, nei vari esercizi che ti verranno assegnati, l’angolo potrà essere espresso in gradi così come in radianti. In questo caso ti sarebbe stato richiesto di trovare la tangente di π/8.
Per risolvere questo piccolo esercizio, è sufficiente applicare la formula di bisezione della tangente.
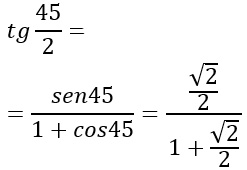
L’ultimo passaggio è stato ottenuto ricordandoci quanto valgono il coseno e il seno di 45. Otteniamo così a numeratore e denominatore una radice quadrata che possiamo semplificare attraverso il metodo della razionalizzazione dei radicali.
Moltiplico e divido quindi per 2 meno radice di 2 sfruttando il prodotto di somma per differenza:
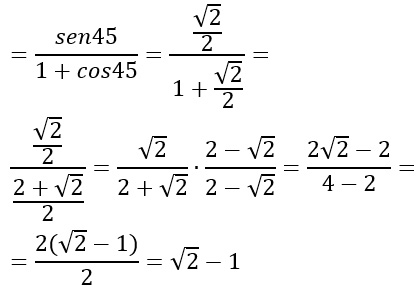
Esercizio 2
Sapendo che tga=2 e che 0<a<π, determinare tg(5/2 a).
Si tratta di un esercizio difficile ma che si basa su una sola riflessione. Non potendo fare la tangente di 5/2 dell’angolo, è necessario dividere quella frazione in due addendi che possiamo risolvere in maniera più semplice. Poiché 5/2 = 1/2 + 2, allora possiamo trasformare la traccia dell’esercizio:
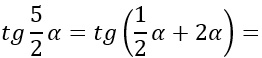
Siamo arrivati ad avere una funzione goniometrica, la tangente, nella forma tg(a+b). E’ necessario quindi applicare le formule di addizione della tangente:
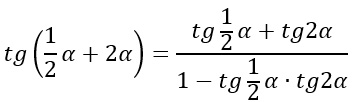
A questo punto possiamo calcolare separatamente la tg2a attraverso le formule di duplicazione e la tga/2 con la formula di bisezione della tangente.
Tenendo presente che valgono le relazioni:
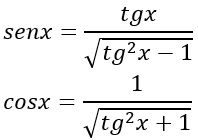
Possiamo sostituire e scrivere:
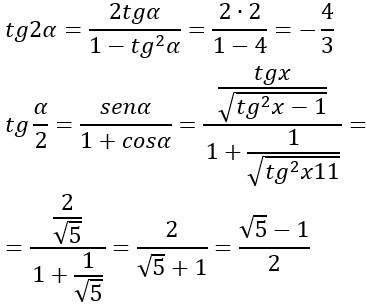
A questo punto è sufficiente andare a sostituire nella traccia modificata in precedenza i risultati così ottenuti.
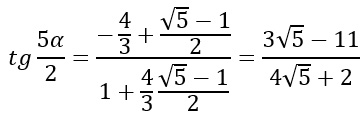
Conclusioni
Durante i compiti in classe le formule di bisezione non compaiono spesso quanto quelle di duplicazione, soprattutto quando il programma diventa più avanzato. Tuttavia restano queste una delle più importanti formule goniometriche e vanno assolutamente imparate a memoria.
Se la lezione è stata di tuo gradimento, se è stata in qualche modo utile o se hai ancora dei dubbi, scrivi in basso nei commenti. Il nostro staff è a tua disposizione.