Come si chiama il poligono con 7 lati? Quali sono le sue proprietà e come posso fare per disegnarlo? – Grazie Milena
In questa lezione, grazie anche alla domanda della nostra lettrice Milena, parliamo di ettagono, il poligono formato da 7 lati. Vedremo in maniera più dettagliata l’ettagono regolare, le sue proprietà, le formule da usare e un esercizio svolto.
Dedicheremo inoltre un capitolo interamente alla costruzione dell’ettagono da fare con squadrette e compasso.
Che cos’è un ettagono?
Significato ed etimlogia
Su alcuni libri viene indicato anche come eptagono e la parola deriva dal greco e può essere scomposta come:
- etta = epta che significa 7;
- gono = gonia che significa angolo.
Definizione
In base a ciò possiamo dire che l’ettagono è il poligono formato da 7 angoli. In genere non si prende come riferimento il numero di angoli, ma il numero di lati. Per cui una definizione alternativa è:
l’ettagono è quella figura geometrica composta da 7 lati.
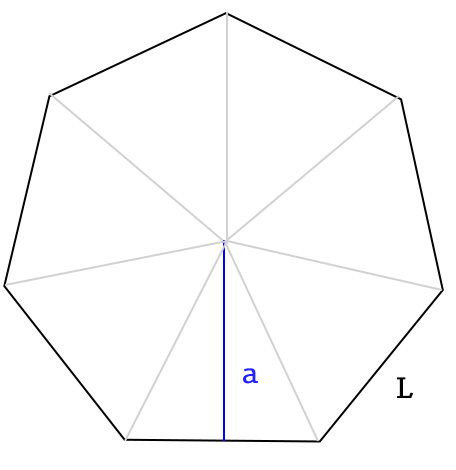
Nel caso in cui i lati sono tutti uguali, allora abbiamo un poligono regolare che chiameremo ettagono regolare.
Proprietà
Dividendo la figura in 7 spicchi come nell’immagine in alto si ottengono 7 triangoli isosceli. Per calcolare gli angoli possiamo ragionare come segue:
- l’angolo al vertice misura 360°:7=51,42°
- poiché la somma degli angoli interni di un triangolo è 180°, allora gli angoli alla base misurano: (180°-51,42°):2=64,29°
Proprietà 1 – Un eptagono può essere sia iscritto che circoscritto ad una circonferenza.
Proprietà 2 – Il centro del poligono si può trovare dall’intersezione degli assi dei suoi lati oppure intersecando tutte le bisettrici dei vertici. Questo punto coincide anche con il centro della circonferenza inscritta o circoscritta.
Proprietà 3 – La somma degli angoli interni di un ettagono è 180(N-2) =180(7-2) = 180·5= 900°
Proprietà 4 – L’angolo di ogni vertice dell’ettagono regolare misura 128,58° (basta dividere 900° per il numero degli angoli, cioè 7)
Formule dell’ettagono
Di seguito elenchiamo le formule da utilizzare negli esercizi sull’ettagono regolare. Indichiamo con p il perimetro, con A l’area, con a l’apotema e L è il lato.
Essendo un poligono regolare, questa figura ha due coefficienti che restano costanti che possono permetterci di calcolare apotema e area dato il lato.
Numero fisso ettagono (f)
E’ un numero che varia a seconda della figura geometrica presa in considerazione. Il dodecagono ha f=1,866, l’ennagono ha f=1,374 e così via.
L’ettagono ha numero fisso pari:
f=1,038
Con il numero fisso è possibile calcolare l’apotema semplicemente avendo il lato della figura.
Costante d’area dell’ettagono (φ)
Il ragionamento è del tutto identico al numero fisso, solo che la costante d’area questa volta serve per determinare l’area noto il lato.
φ=3,634
Perimetro dell’ettagono
Essendo un poligono regolare, è possibile determinarne il perimetro semplicemente moltiplicando il lato per il numero dei lati. Quindi in questo caso abbiamo:
P=7L
Area dell’ettagono
Ci sono due metodi per poter calcolare la superficie di questa figura geometrica piana a seconda che sia noto il lato o l’apotema.
- Se è noto l’apotema:
 Si moltiplica il perimetro per l’apotema e si divide il risultato per 2.
Si moltiplica il perimetro per l’apotema e si divide il risultato per 2. - Se è noto il lato:
A=φ·L²
E’ necessario moltiplicare il quadrato del lato per il coefficiente d’area.
Ovviamente da queste è possibile ricavare le formule inverse per ottenere così la misura del lato o dell’apotema.
Costruzione dell’ettagono
Come si disegna questa figura geometrica con foglio, squadre, compasso e matita? Ecco il tutorial spiegato passo passo.
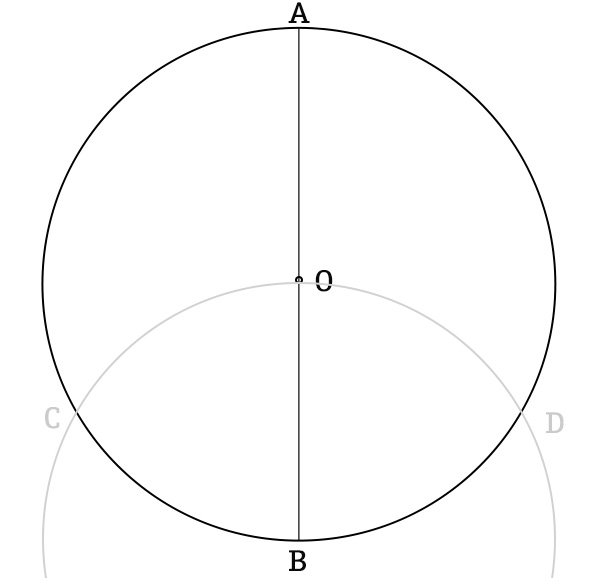
- Traccia il diametro AB della circonferenza circoscritta. Con il compasso apertura BO, centro in B, trova i punti C e D sulla circonferenza.

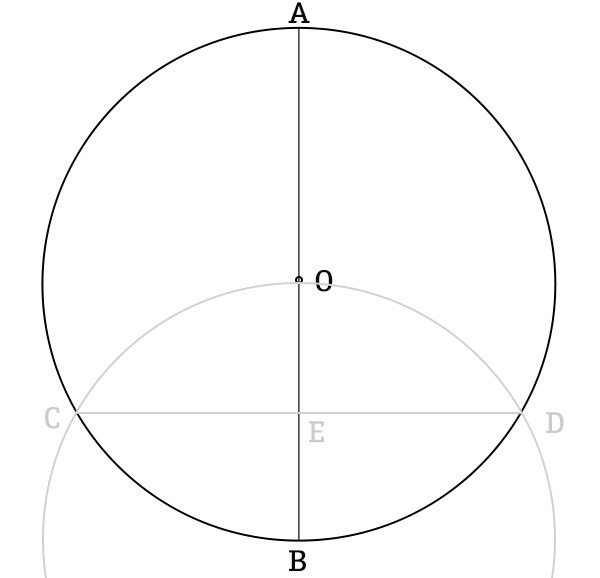
- Traccia la corda CD così da intersecare il diametro nel punto E

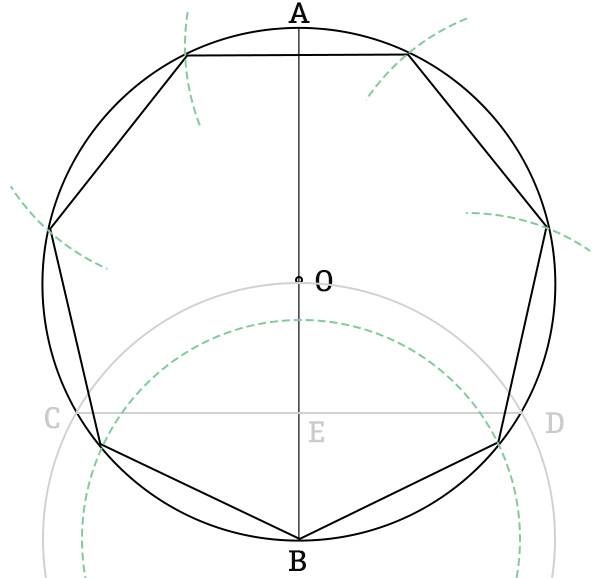
- La lunghezza CE è il lato L dell’ettagono regolare. Per cui da B possiamo disegnare sette archi di lunghezza L.

Esercizio
Calcolare perimetro e area dell’ettagono regolare con lato pari a 10 cm.
Svolgimento
Per il calcolo del perimetro basta che moltiplico L per 7. Ottengo quindi che:
P= 10 cm · 7 = 70 cm
Per l’area sfruttiamo la costante d’area φ
A=φ·L² = 3,634 · 10² = 363,4 cm²
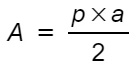 Si moltiplica il perimetro per l’apotema e si divide il risultato per 2.
Si moltiplica il perimetro per l’apotema e si divide il risultato per 2.