In questa lezione vedremo come si risolvono gli esercizi sulla retta nel piano cartesiano, cercando di svolgere insieme degli esercizi svolti con l’aiuto di formulari e di alcuni trucchi per rendere tutto più facile.
Ti consigliamo vivamente, prima di provare a risolvere i problemi sulla retta, di avere ben chiara la parte teorica. Nel caso in cui hai ancora qualche dubbio sulla formule e sulle equazioni della retta nel piano cartesiano, dai un’occhiata alla nostra lezione (leggi i nostri APPUNTI SULLA RETTA). Ecco le tracce degli esercizi svolti che ti proponiamo. Cliccando su ogni traccia, andrai direttamente allo svolgimento dell’esercizio.
- Determinare l’equazione della retta passante per un punto P(-1;-2) e parallela alla retta di equazione y=4/3 x +31/3
- Calcolare l’equazione della retta passante per i punti A(1;-1) e B(2;1). Dopo aver disegnato il grafico calcolare la distanza con il punto P(3;2)
- Calcolare il punto di intersezione della retta 5x+2y=8 con la retta passante per i punti A(0;2) e B(3;0)
- Determinare l’area del triangolo ABC, triangolo di vertici nei punti A(1;0), B(2;-3) e C(0;-1) (verifica di che tipo di triangolo si tratta)
- Calcola l’altezza AH del triangolo avente per vertici A(-3;-1) B(-1;7) e C(5;1)
Esercizio 1)
La traccia ci spiega che la nostra retta passa per un punto P(-1;-2) e ci fornisce una retta parallela con equazione y=4/3x+31/3. Vuol dire che abbiamo a disposizione due dati: l’appartenenza e il parallelismo. Poiché quando si studia la retta nel piano cartesiano le incognite sono 2, cioè m (il coefficiente angolare) e q (intercetta sull’asse delle ordinate) possiamo risolvere il problema.
Una delle prime verifiche che consigliamo sempre di fare ai nostri studenti è di controllare che il numero di dati sia pari al numero di incognite.
Il primo passo è quindi quello di sfruttare il parallelismo. Due rette parallele, infatti, per definizione hanno lo stesso coefficiente angolare. Questo significa che m=4/3.
Il passo successivo è di sfruttare l’appartenenza del punto P. Se nell’esercizio la retta passa per un punto, vuol dire che quest’ultimo vi appartiene. Praticamente è possibile andare a sostituire le sue coordinate (l’ascissa e l’ordinata), nell’equazione della retta y=mx+q.

In questo modo ho ottenuto il coefficiente angolare e la q della retta che avrà quindi equazione y=4/3x-2/3. In geometria analitica, il disegno è una parte importante di ogni esercizio da risolvere. Nelle scorse lezioni abbiamo visto come disegnare una retta nel piano cartesiano, per cui non dovresti avere difficoltà in questo esercizio a disegnare il punto P e la retta parallela della traccia. E’ un esercizio che lasciamo a te…
Esercizio 2)
La traccia ci chiede, sostanzialmente di calcolare l’equazione della retta passante per 2 punti A(1;-1) e B(2;1). Abbiamo già visto nella parte teorica che esiste una specifica formula, per cui l’esercizio è molto facile da risolvere: basta sostituire le coordinate dei punti. Ecco come fare:

Come puoi vedere sulla destra ti abbiamo riportato anche il grafico della retta che ci siamo calcolati.
Esercizio 3)
Il terzo esercizio da risolvere riguarda l’intersezione tra due rette. La prima di queste viene già data dalla traccia, mentre la seconda calcolarla come passante per due punti. Cioè si inizia ripetendo esattamente quello che abbiamo fatto nell’esercizio 2.

Una volta calcolata quindi l’equazione della seconda retta non ci resta che risolvere l’esercizio scrivendo il sistema delle due equazioni:

Per risolvere il sistema è stato usato il metodo di sostituzione e, dopo qualche semplice calcolo algebrico e minimo comune multiplo, si arriva facilmente alla soluzione del problema.
Esercizio 4)
La traccia ti fornisce 3 punti, cioè i 3 vertici di un triangolo. La prima cosa che possiamo fare è disegnare il grafico e calcolare la distanza tra questi due punti, in modo da capire se ci troviamo di fronte ad un triangolo particolare (es. Isoscele, Scaleno o Equilatero)

Per calcolare il risultato finale di BC abbiamo eseguito portato fuori il 4 dalla radice (se hai dubbi su come è stato risolto, guarda la lezione sulle regole delle radici). Per calcolare l’area di un triangolo avendo i lati posso usare la Formula di Erone ma avrei dei calcoli piuttosto complessi con radici di radici. In matematica c’è un solo grande trucco e vale come regola generale: scegliere sempre la strada più semplice e mai complicarsi la vita.
Ecco perché è preferibile calcolare l’altezza relativa ad un lato e poi semplicemente sfruttare la formula classica Base x Altezza diviso 2 per l’Area dei Triangoli.
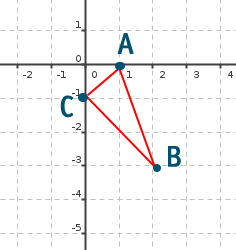
Osservando il disegno in alto possiamo notare che potrebbe sussistere una perpendicolarità tra le rette AC e CB. Per verificarla devo trovare le equazioni delle rette AC e CB.
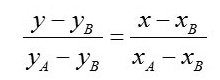
dove A(1;0) e C(0;-1)
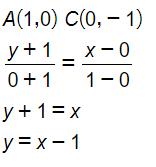
Ripetiamo il calcolo per la retta BC
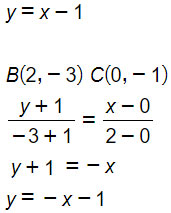
Hai notato che le rette AC e BC hanno coefficiente angolare pari a 1 e -1. Poiché mAC=-1/mBC allora si tratta di due rette perpendicolari. Quindi per calcolare l’area basta moltiplicare A=ACxBC/2=(√2)(2√2)/2 → A=2.
Esercizio 5)
Dato che si tratta di una ripetizione dell’esercizio precedente, lasciamo a te risolvere a casa questo esercizio. Ricordati quindi di calcolare l’equazione della retta passante per BC e di fare poi la distanza A da quest’ultima. Si tratta di pochi semplici passaggi. Se dovessi tuttavia avere problemi a trovare una soluzione in maniera semplice o se comunque ti restano dei dubbi, il nostro staff è a tua completa disposizione.
Contattaci per chiederci ed esponici le tue difficoltà.
mi servirebbe sapere il risultato dell’ ultimo esercizio
Il risultato è 5rad2 (cioè circa 7.07)
AH=5sqrt(2)
retta BC:y=6-x
Vorrei una mano sull’esercizio 5
Mi serve aiuto
Viste le tante richieste, inserisco il risultato dell’esercizio 5 di seguito:
