Benvenuto in questa esercitazione interamente dedicata agli esercizi sulla parabola. Troverai all’interno di questa lezione tanti esempi svolti e commentati per imparare ad applicare le formule che hai studiato in maniera semplice e chiara.
In tutti gli esercizi svolti sulla parabola, potrai trovare un commento completo e una guida alla risoluzione con i vari passaggi spiegati passo passo. Ovviamente è importante che abbia già studiato qual è l’equazione della parabola, come si calcolano le coordinate del vertice, del fuoco e degli altri elementi geometrici caratteristici. Se hai già confidenza con la parte teorica, allora sei pronto ad iniziare questa esercitazione.
Approfondimenti: tabella riepilogativa sulla parabola
Esercizi parabola per per 3 punti
Calcolare l’equazione della parabola con asse parallelo all’asse y e passante per i punti A(-1;0), B(0;3) e C(-3;6).
Svolgimento
La parabola deve avere equazione del tipo:
y=ax²+bx+c
A questo punto bisogna imporre l’appartenenza di ogni singolo punto alla parabola. Come si fa? Semplicemente sostituendo le coordinate di ogni singolo punto nell’equazione generale appena indicata. Quindi, indicando con la lettera greca γ (gamma) la parabola, possiamo scrivere che:
A(-1;0) ∈ γ → 0=a(-1)²+b(-1)+c → 0=a-b+c
B(0;3) ∈ γ → 3=a(0)²+b(0)+c → c=3
C(-3;6) ∈ γ → 6=a(-3)²+b(-3)+c → 6=9a-3b+c
Abbiamo praticamente ottenuto un sistema di primo grado con tre equazioni. Possiamo risolvere con il metodo della sostituzione, ma se preferiamo anche con somma o differenza, o Cramer.
a=b-3
c=3
2=3(b-3)-b+1
a=2
c=3
b=5
Per cui il risultato finale diventa:
y=2x²+5x+3
Esercizi parabola noti il fuoco e la direttrice
Scriviamo l’equazione della parabola avente fuoco F(-1;0) e direttrice d:y=2.
L’esercizio può essere risolto in due modi differenti.
- Costruiamo un sistema di primo grado, come nell’esercizio sulla parabola svolto prima. Su un rigo mettiamo xf=-b/2a=-1, sul secondo rigo mettiamo yf=0=(-Δ+1)/4a e nel terzo rigo usiamo l’equazione della direttrice. d:y=(-Δ-1)/4a=2
- Il secondo metodo invece è più rapido e sfrutta direttamente la definizione di parabola, intesa come il luogo dei punti equidistanti dal fuoco e dalla direttrice.
Risolviamo con proprio con il secondo metodo indicando con P(x,y) il generico punto della parabola. Disegniamo i dati a disposizione ricordando che se la direttrice è una retta orizzontale (come in questo caso), allora la parabola ha asse parallelo alle y.
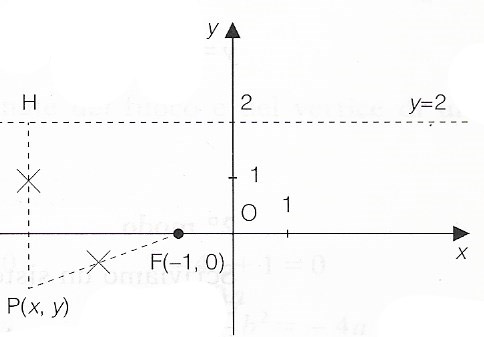
PH=PF
Da notare che il segmento PH non è altro che la distanza punto retta a P fino a d:y=2. PF invece si calcola con la formula della distanza tra due punti. Visto che nella formula della distanza c’è una radice quadrata, eleviamo entrambi al quadrato.
PH²=PF²
(y-2)² = (x+1)²+y²
y²-4y+4=x²+2x+1+y²
-4y=x²+2x- 3
y=(-1/4) x² – 1/2 x + 3/4
Esercizi parabola noti fuoco e vertice
Determiniamo l’equazione della parabola avente il fuoco F(2;1) e il vertice V(2;-1).
Questo esercizio sulla parabola si può risolvere in due modi.
- Il vertice si trova nel punto medio del segmento FH perpendicolare alla direttrice. Perciò la direttrice ha equazione y=-3. Noti il fuoco e la direttrice possiamo procedere come nell’esercizio svolto precedente. Lasciamo a te la risoluzione come esercitazione.
- Scriviamo un sistema utilizzando le formule relative alla coordinate del fuoco e del vertice. Indicata con y=ax²+bx+c l’equazione della parabola richiesta, si ha:
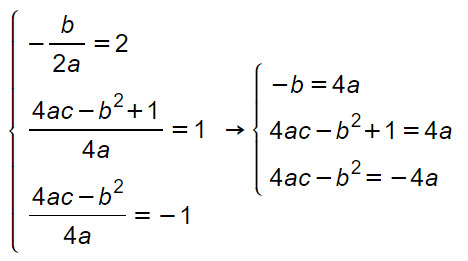
Sottraiamo membro a membro la seconda e la terza equazione, per ottenere dopo pochi subito l’incognita a e poi di conseguenza tutte le altre.
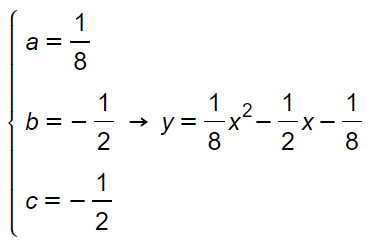
Esercizi parabola noti vertice e direttrice
Determiniamo l’equazione della parabola avente vertice V(0;3) e direttrice d:x=1/4.
La parabola ha equazione del tipo x=ay²+by+c. Infatti la direttrice è parallela all’asse y, per cui l’asse di simmetria sarà orizzontale. Scriviamo quindi un sistema utilizzando i dati messi a disposizione dalla traccia, così come fatto negli esercizi svolti precedenti.
-b/2a=3
(4ac-b²)/4a=0
4ac-36a²-1=a
b=-6a
c=9a
a=-1
a=-1
b=6
c=-9
Perciò l’equazione richiesta è x=-y²+6y-9
Esercizi parabola passante per 1 punto e noto il fuoco
Determiniamo l’equazione della parabola avente asse parallelo all’asse y, fuoco F(-1/4;-1) e passante per il punto P(0;-1).
L’equazione della parabola è del tipo:
y=ax²+bx+c
Poiché F(-1/4;-1), possiamo scrivere un sistema di due incognite con le formule delle sue coordinate:
xF=-1/4=-b/2a
yF=-1=(4ac-b²+1)/4a
b=1/2a
c=(1/4 a² – 1 – 4a) / 4a
Sostituiamo i valori di b e c, espressi in funzione di a, nell’equazione della parabole:
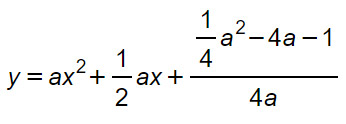
Imponiamo che la parabola passi per il punto P(0;-1) per cui sostituiamo le sue coordinate nell’equazione appena scritta.
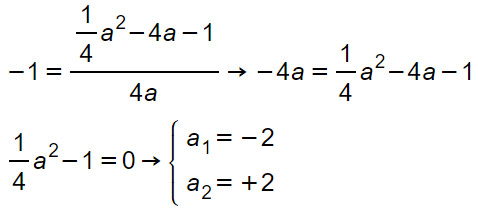
Come puoi osservare dal risultato, abbiamo ottenuto due valori del coefficiente a. Questo vuol dire che ci sono due parabole che soddisfano il sistema.
γ1: y=-2x²-x-1
γ2: y=2x²+x-1
Esercizio parabola con il parametro k
Data la parabola di equazione
y = kx² + (k+1)x – 2
determiniamo per quali valori di k:
- la parabola passa per P(1;2)
- il suo vertice appartiene alla retta y=x+1
- il suo vertice ha ascissa positiva
- il suo vertice si trova nel terzo quadrante
Svolgimento
Primo punto
Le coordinate del punto P devono soddisfare l’equazione della parabola. Perciò sostituiamo le sue coordinate al posto della x e della y dell’equazione dataci dalla traccia dell’esercizio.
2=k+k+1-2
2k=3
k=3/2
Secondo punto
Le coordinate del vertice in funzione di k sono:
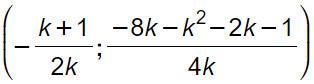
Imponiamo che tali coordinate soddisfino l’equazione y=x+1. Per cui ottengo:
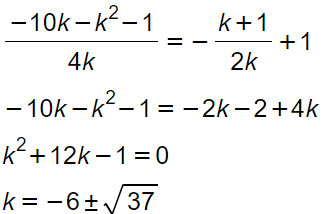
Da notare che nel penultimo passaggio abbiamo ottenuto un’equazione di secondo grado, risolta con il metodo del delta.
Punto terzo
L’ascissa del vertice è xv=-[(k+1)/2k], perciò deve essere valida la disequazione.
-[(k+1)/2k]>0
(k+1)/2k<0
Si ottiene un falso sistema con:
k+1>0 → k>-1
2k>0 → k>0
Si mette tutto su un piccolo grafico applicando la regola dei segni + – e si prendono i segni negativi.
-1<k<0
Punto quarto
Le coordinate del vertice devono essere entrambe negative, perciò, poiché
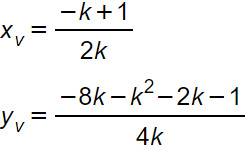
Imponiamo entrambi i valori minori di zero. Per cui, proseguendo con l’esercizio, otteniamo:
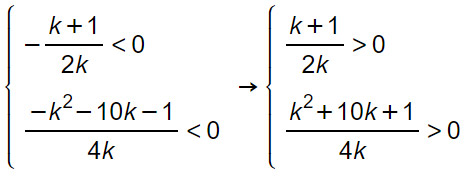
Abbiamo quindi semplicemente cambiato i segni e invertito i versi della disequazione.
- La prima disequazione è verificata, facendo un breve falso sistema, per -1<k U k>0;
- La seconda disequazione:
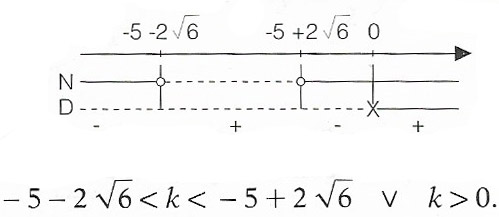
N>0 → k²+10k+1>0 → k<-5-2√6 U k>-5+2√6
D>0 → k>0
Si tratta di una disequazione fratta, per cui dopo il falso sistema si mette sul grafico e si prendono valori positivi.

Mettiamo a questo punto a sistema le due disequazioni, osservando il seguente schema.
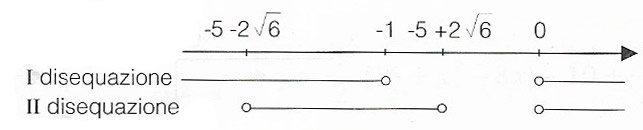
Per cui il sistema è verificato per:
-5-2√6<k<-1 U k>0.