In questa pagina vedremo una serie di esercizi sulle equazioni goniometriche. Cominceremo dalla risoluzione delle forme elementari, aumentando man mano il livello di difficoltà. Gli esercizi sono svolti e commentati passo passo, così che tu possa capire anche il ragionamento che ci ha permesso di trovare la soluzione.
La regola base da seguire
Prima di passare agli esercizi svolti è utile fare un brevissimo ripasso sul metodo di risoluzione che abbiamo visto nella lezione sulle equazioni goniometriche.
Esercizi equazioni goniometriche elementari
– Esercizio 1
2senx=1
Otteniamo subito senx=-1/2 e, visto che sen210=-1/2, possiamo scrivere che l’equazione è soddisfatta per:
x=210°+2k·180° ∪ x=330°+2k·180°
Applicando la conversione gradi radianti, il risultato dell’esercizio è:
x=7/6π+2kπ ∪ x=11/6π+2kπ
Ricordiamo che se α è un angolo per cui senα=m, anche l’angolo (180°-α) ha seno uguale a m. Se hai bisogno di un approfondimento sull’argomento ti consigliamo di leggere la lezione sugli archi associati. Nel nostro caso α=210°, 180°-α=180°-210°=-30° e quest’ultimo angolo non è altro che l’angolo di 330°.
– Esercizio 2
cos(x-30°)=√3/2
Poiché cos30°=√3/2, possiamo scrivere:
x-30°=30°+2k·180° ∪ x-30°=-30°+2k·180°
Spostando il 30° che compare al primo membro a destra dell’equazione goniometrica, otteniamo:
x=60°+2k·180° ∪ x=2k·180°
– Esercizio 3
tgx=√3
Poiché tg(π/3)=√3, possiamo scrivere le soluzioni come segue:
x=π/3+kπ
Da notare come la periodicità della funzione tangente sia espressa in questo caso da kπ, mentre nel seno e coseno è data da 2kπ. Questo perché la tangente è periodica per ogni 180°.
– Esercizio 4
2 sen(x+π/4)=√2
Il primo passaggio è quello di spostare il 2 al secondo membro dell’equazione. Otteniamo quindi:
sen(x+π/4)=√2/2
Ricordando che il seno di 45° vale proprio √2/2, possiamo quindi dire che l’esercizio sull’equazione goniometrica si risolve per:
x+π/4=π/4+2kπ ∪ x+π/4=3/4 π + 2kπ
Ossia:
x=2kπ ∪ x=π/2+2kπ
– Esercizio 5
tg(2x-30°)
Poiché tg135°=-1, scriviamo le soluzioni come segue:
2x-30°=135°+k·180°
da cui otteniamo:
2x=165°+k·180°
Dividendo tutto per 2, si arriva alla soluzione finale:
x=82°30’+k·90°
Esercizi equazioni goniometriche riconducibili alle elementari
– Esercizio 1
8sen³x+1=0
La prima operazione da fare è provare a scomporre questo polinomio di terzo grado. Troverai nelle lezioni sulle scomposizioni di polinomi anche una regola che vale per la somma di cubi.
x³ + a³ = (x+a)(x²-ax+a²)
Allora il nostro esercizio diventa:
(2senx+1)(4sen²x-2senx+1)=0
per la legge dell’annullamento del prodotto, possiamo individuare le soluzioni dell’equazione svolta ponendo:
2senx+1=0 ∪ 4sen²x-2senx+1=0
Otteniamo così due piccoli esercizi sulle equazioni goniometriche: il primo è elementare. Dalla prima equazione otteniamo:
senx=-1/2
da cui x=7/6π+2kπ ∪ x=11/6π+2kπ
Dalla seconda equazione non otteniamo alcuna radice reale. Se provi infatti ad applicare le regole delle equazioni di secondo grado, avrai un delta negativo. Per cui non ci sono soluzioni reali.
– Esercizio 2
2cos²x-cosx+1=0
Ponendo cosx=y, otteniamo un’equazione di secondo grado.
2y²-y-1=0
Le due soluzioni, applicando il metodo del delta, sono:
y=-1/2 ∪ y=1
Sostituendo di nuovo y=cosx, perveniamo così a due mini esercizi sulle equazioni goniometriche elemetari:
cosx=-1/2 e cosx=1
le quali risultano verificate rispettivamente per:
x=±2/3π+2kπ (soluzioni di cosx=-1/2)
x=2kπ (soluzioni di cosx=1)
– Esercizio 3
3tg²x-1=0
Iniziamo a scomporre il binomio della traccia, applicando la regola della differenza di quadrati. Attenzione: affinché l’equazione abbia un significato è che x≠90°+k180° (condizione di esistenza)
(√3tgx-1)(√3tgx-1)=0
Per la legge dell’annullamento del prodotto possiamo scrivere che:
√3tgx-1=0 → tgx=√3/3 → x=30°+kπ
√3tgx+1=0 → tgx=-√3/3 → x=150°+kπ
Da notare come a questo passaggio (che ti abbiamo segnato in blu) siamo arrivati attraverso una razionalizzazione del radicale. Si trovava infatti radice di 3 al denominatore ed abbiamo provveduto a portarlo al numeratore.
Il risultato di questo esercizio è quindi:
x=30°+kπ ∪ x=150°+kπ
– Esercizio 4
cotg²x-cotgx=0
Perché l’equazione abbia significato deve essere x≠kπ (condizione di esistenza)
Possiamo effettuare la messa in evidenza totale, da cui otteniamo:
cotgx(cotgx-1)=0
Per la legge dell’annullamento del prodotto possiamo determinare le soluzioni dell’equazione assegnata risolvendo le equazioni elementari:
cotgx=0 e cotgx-1=0
La prima è soddisfatta per x=π/2+kπ.
Le seconda è soddisfatta per x=π/4+2kπ.
– Esercizio 5
2sen³x-5sen²x+senx+2=0
Guarda la forma di questo esercizio… non ti ricorda in tutto e per tutto un’equazione di terzo grado? Proviamo infatti a sostituire senx=y ed otteniamo:
2y³-5y²+y+2=0
Possiamo scomporre il primo membro dell’equazione utilizzando la regola di Ruffini. Da notare che y=1 è uno zero del polinomio (cioè sostituendo y=0 otteniamo l’identità 0=0, per cui
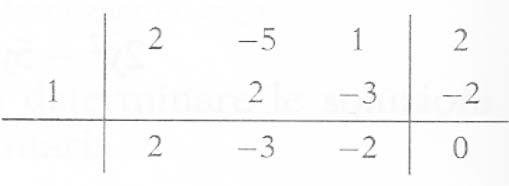
(y-1)(2y²-3y-2)=0
sostituendo di nuovo senx=y, otteniamo il prodotto:
(senx-1)(2sen²x-3senx-2)=0
da cui, per la legge dell’annullamento del prodotto:
senx=1 ∪ 2sen²-3senx-2=0
Dall’equazione senx=1, otteniamo le soluzioni x=π/2+2kπ
Dall’equazione 2sen²-3senx-2=0 otteniamo:
senx=-1/2 ∪ senx=2 (abbiamo semplicemente usato la regola del delta per le equazioni di secondo grado)
Per cui:
senx=-1/2 → x=7/6π+2kπ ∪ x=11/6π+2kπ
senx=2 → nessuna soluzione, perché il seno non può essere maggiore di +1.
L’esercizio svolto quindi ammette soluzioni:
x=π/2+2kπ ∪ x=7/6π+2kπ ∪ x=11/6π+2kπ