Categoria: La retta

RETTA GEOMETRIA ANALITICA – hai dubbi o problemi sulla retta e cerchi degli approfondimenti o dei chiarimenti? In questa pagina vedremo tutto quello che c’è da sapere sullo studio della retta in geometria analitica.

Senza perderci tempo in chiacchiere partiamo subito dalla definizione per poi analizzare l’equazione della retta (implicita ed esplicita), le relative formule e caratteristiche geometriche.

Definizione

La retta è un insieme infinito di punti allineati nel piano

Questo significa che la retta può essere considerato come una linea retta formata da tantissimi punti ravvicinati che non hanno né un inizio né una fine.

Approfondimento: Definizione di retta – l’ente fondamentale della geometria

Come si rappresenta la retta nel piano?

Come tutte le figure rappresentate sugli assi cartesiani, anche la retta in geometria analitica si esprime attraverso un’equazione con due incognite: x e y.

Approfondimento: come disegnare una retta nel piano cartesiano

La retta come luogo geometrico

Su molti libri di geometria analitica, si trovano alcune definizioni che indicano la retta come un luogo geometrico di punti che rispettano un’equazione lineare. Che vuol dire?

Che assegnato un generico punto P di coordinate (xp ; yp) questo appartiene alla retta solo se le sue coordinate ne verificano l’equazione.

Appartenenza di un punto alla retta

Per verificare se un punto appartiene a una retta, inserisci le sue coordinate nell’equazione della retta. Se questa è verificata (cioè ti esce un numero a sinistra uguale allo stesso numero a destra, es: 3=3), allora l’appartenenza è verificata.

Esempio:

P(1;2)

retta r: y=x+1

Per verificare che P appartiene a r, sostituiamone le coordinate nell’equazione:

y=x+1 → 2=1+1 → 2=2 → Appartenenza verificata

Equazione della retta

Abbiamo dedicato un’intera lezione a come la retta viene rappresentata nel piano inclinato. Ci sono sostanzialmente due modi.

Formula implicita

ax+by+c=0

Dove a,b e c sono 3 coefficienti, cioè tre numeri che permettono l’individuazione univoca della retta nel piano. Si tratta sostanzialmente di un’equazione lineare, cioè di un polinomio di primo grado uguale a zero.

Formula esplicita

y=mx+q

E’ sicuramente la formula più utilizzata perché ci dà maggiori informazioni.

m = coefficiente angolare della retta = esprime la sua pendenza rispetto all’asse delle ascisse.

q = termine noto = è l’ordinata che si ottiene dall’intersezione della retta con l’asse y.

Rette orizzontali e verticali

Rette orizzontali: hanno l’equazione del tipo y=k

Rette verticali: hanno l’equazione del tipo x=k

dove k è un generico numero.

COME RICORDARLO: in genere l’orizzontale è associato all’asse x, mentre la direzione verticale è associata all’asse y. Per ricordarti le rette orizzontali, ricordati di invertire questo ragionamento.

La retta orizzontale si rappresenta con y uguale a un numero. La retta verticale si rappresenta con x uguale a un numero.

Rette parallele e perpendicolari

L’equazione esplicita della retta in geometria analitica ci permette di ottenere l’inclinazione e quindi, indirettamente, l’angolo che si forma rispetto all’asse x.

Per questa ragione possiamo dire che due rette sono parallele se hanno lo stesso coefficiente angolare. Al contrario, invece, due rette sono perpendicolari tra loro se la m della prima retta è l’antireciproco della m della seconda retta. Per esempi e formule ti rimandiamo alla lezione di approfondimento:

Vai alla lezione: Rette parallele e perpendicolari sul piano cartesiano

Retta per un punto e con m noto

Nel caso in cui ci venga data l’inclinazione della retta, quindi il coefficiente angolare, e un punto P(xp;yp) per cui essa passa, la formula da utilizzare è:

y-yp=m(x-xp)

Per esempi e ulteriori spiegazioni, abbiamo creato una lezione di approfondimento apposta.

Vai alla lezione: Retta passante per un punto con m noto

Retta passante per due punti

Nel caso in cui io abbia due punti A e B, l’equazione della retta si può determinare risolvendo questa semplice equazione:

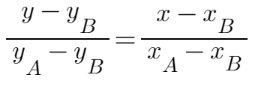
Per esempi e spiegazioni vai alla lezione di approfondimento.

Vai alla lezione: retta passante per due punti

Distanza di un punto da una retta

La distanza è il segmento che unisce perpendicolarmente il punto con la retta. Si calcola utilizzando la formula:

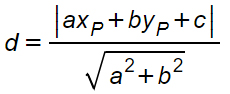
Per approfondimenti ed esempi, vai alla lezione sulla distanza punto retta.