Categoria: Ellisse
L’ellisse è il luogo dei punti del piano cartesiano per i quali è costante la somma delle distanze da due punti fissi detti fuochi. Nelle scuole, l’ellisse viene studiato nel programma di geometria analitica subito dopo la parabola.
In questa lezione vedremo tutte le principali formule dell’ellisse. Partendo dalla definizione, vedremo sono le equazioni di questa figura geometrica, che cos’è e come si calcolano fuochi ed eccentricità.
Oltre all’equazione dell’ellisse vedremo alcuni esercizi svolti per mettere in pratica quanto imparato
Definizione di ellisse
L’ellisse in geometria analitica viene definita come il luogo geometrico dei punti per cui resta costante la somma delle distanze da due punti fissi detti fuochi.
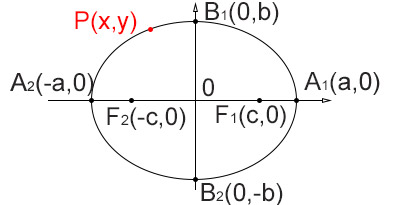
dove:
- A1, B1, A2, B2 = vertici dell’ellisse
- F1 e F2 = fuochi dell’ellisse
- O = centro dell’ellisse
Analizzando la figura in alto, la definizione sta ad indicare che la distanza di un qualsiasi punto appartenente all’ellisse (ad esempio il generico P) dal primo fuoco F1, sommato alla distanza di P dal secondo fuoco F2 resta sempre costante.
PF1+PF2 = costante
Come puoi vedere in figura, l’ellisse ha due assi di simmetria. Nei programmi delle scuole superiori si studia solo l’ellisse con assi di simmetria paralleli ad uno dei due assi cartesiani. Si può tranquillamente arrivare all’equazione dell’ellisse inclinata o traslata con pochi piccoli accorgimenti di cui però non ci occuperemo in questa lezione.
Equazione ellisse
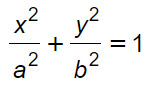
a, b e c sono coefficienti numerici che stanno ad indicare rispettivamente l’ascissa del primo vertice, l’ordinata del secondo vertice, l’ascissa del fuoco.
Si dimostra che vale la formula:
b²=a²-c²
Le coordinate di ogni punto della figura devono soddisfare l’equazione dell’ellisse in forma canonica (o forma normale).
Considerazioni sulla formula dell’ellisse
Si fa notare che l’equazione dell’ellisse è un’equazione di secondo grado a due incognite, x e y. Poiché è priva del termine di primo grado e di xy, allora rappresenta una curva simmetrica rispetto agli assi cartesiani e all’origine.
Proprio come accadeva con l’equazione della circonferenza nel piano cartesiano, l’equazione canonica vista sopra non è una funzione. Questo perché se provi a tirare una linea verticale, vedrai che ci sono due punti di intersezione con la figura. Questo significa che per ogni valore di x sono presenti 2 punti di y e ciò viola la definizione di funzione.
Intersezioni con gli assi
Le intersezioni della figura con gli assi cartesiani, in particolare con l’asse delle ascisse e delle ordinate, generano rispettivamente i punti A1, A2, B1, B2, noti come vertici dell’ellisse.
Il segmento A1A2, contenente i fuochi, è detto asse maggiore. Il segmento B1B2, viene detto invece asse minore ed è perpendicolare al primo.
- La misura dell’asse maggiore è 2a
- La misura dell’asse minore è 2b
Il punto di intersezione degli assi viene chiamato centro dell’ellisse.
Eccentricità
E’ un parametro che indica lo schiacciamento dell’ellisse sull’asse delle x. Si definisce eccentricità il rapporto
e = c / a
Poiché a>c, allora l’eccentricità e è un numero sempre maggiore di 1. Si dimostra anche che questo parametro può essere espresso in funzione di a e b attraverso la seguente formula.
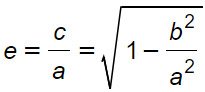
I due casi limite sono:
- l’ellisse è “tanto schiacciata”, per cui e=1. In questo caso si dice che la figura “degenera” in un segmento.
- l’ellisse non ha eccentricità, per cui e=0. In questo caso si dice che la figura “degenera” in una circonferenza.
Ellisse con asse maggiore verticale
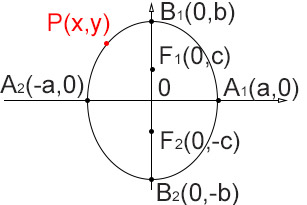
Se i fuochi si trovano sull’asse y allora nell’equazione dell’ellisse cambiano le relazioni tra i coefficienti. In questo caso infatti
a< b
In questo caso l’asse maggiore è il segmento B1B2, di misura 2b, e l’asse minore è il segmento A1A2, di misura 2a. L’eccentricità è invece pari a:
e = c / b
L’ellisse, quale che sia la sua posizione nel piano cartesiano, è sempre simmetrica rispetto ai suoi due assi perpendicolari e al loro punto di intersezione.
Quando l’equazione dell’ellisse è in forma canonica, gli assi di simmetria coincidono con gli assi cartesiani, per cui l’equazione canonica è anche nota come equazione dell’ellisse riferita ai suoi assi e al suo centro.
Esempi
L’equazione di un’ellisse con asse maggiore uguale a 6 e asse minore uguale a 4, può essere scritta nella forma canonica x²/a²+y²/b²=1.
Se i fuochi sono sull’asse x, poiché la misura dell’asse maggiore è uguale a 2a e dell’asse minore 2b (a>b), possiamo calcolare che:
- a=6/2=3
- b=4/2=2
Per cui l’equazione cercata è:
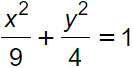
Se invece i fuochi sono sull’asse y, la misura dell’asse maggiore è 2b e quello minore 2a (a<b). Quindi poiché a=2 e b=3, l'equazione cercata è:
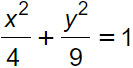
Conclusioni e approfondimenti
In questa pagina abbiamo visto in maniera schematica tutte le formule e le nozioni base riguardanti l’ellisse nel piano cartesiano. Di seguito trovi la lista con tutte le lezioni di approfondimento in cui troverai tantissimi esercizi svolti con cui esercitarti.