Categoria: La circonferenza

La circonferenza nel piano cartesiano è il luogo geometrico dei punti equidistanti da un punto fisso detto centro. Tale distanza viene detta raggio.

In questa lezione vedremo una sintesi di tutti i concetti principali e delle formule sulla circonferenza che si studiano nel programma di geometria analitica. Troverai tanti link di approfondimento in cui verranno trattati gli argomenti in maniera più dettagliata con degli esercizi svolti e commentati.

Equazione cartesiana della circonferenza

Dati  il centro delle circonferenza C(α;β) e la misura r del raggio,  indichiamo con P(x,y) il punto generico appartenente alla circonferenza.

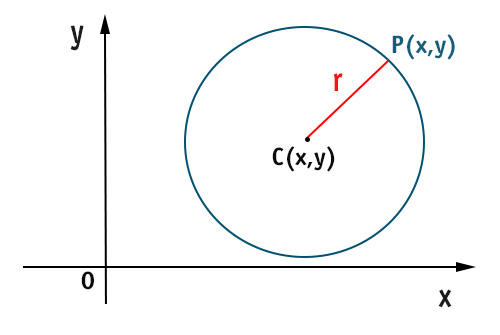
L’equazione della circonferenza è data dalla formula:

(x-α)²+(y-β)²=r²

Andando a svolgere tutti i quadrati di binomio e facendo una serie di semplificazioni, si ottiene l’equazione cartesiana della circonferenza in forma canonica:

x²+y²+ax+by+c=0

Si tratta di un’equazione di secondo grado a due incognite. Il raggio della circonferenza è pari a:

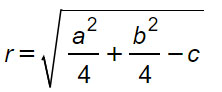
Mentre il centro è pari a:

C(-a/2;-b/2)

Se il centro della circonferenza coincide con l’origine O degli assi cartesiani, allora C(0;0) per cui l’equazione diventa:

x²+y²=r²

Se inoltre il raggio è pari a 1, si ottiene quella che viene chiamata circonferenza goniometrica, un’importante figura geometrica su cui si basa tutto il programma di trigonometria.

Posizione della circonferenza nel piano cartesiano

Se qualcuno dei coefficienti a,b, c dell’equazione canonica vista sopra si annulla, allora la circonferenza da essa rappresentata assume particolari posizioni rispetto agli assi cartesiani.

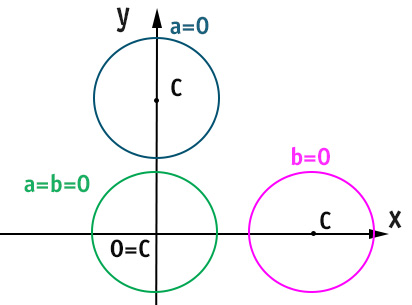
• Se a=0, allora l’ascissa del centro -a/2=0, perciò il centro si trova sull’asse y.
• Se b=0, allora l’ordinata del centro -b/2=0, perciò il centro si trova sul’asse x.
• Se a=b=0, allora il centro della circonferenza ha coordinate nulle, per cui coincide con l’origine degli assi.
• Se c=0, allora il punto 0(0;0) soddisfa l’equazione. Se provi infatti a sostituire il punto 0 in x²+y²+ax+by=0, otterrai l’identità 0=0. Quindi la circonferenza passa per 0.
• Ci sono infine i casi misti: se c=0 e a=0 allora passa per l’origine e il centro è sull’asse y. Se c=0 e b=0 allora passa per l’origine e il centro è sull’asse x.

Posizioni di una retta rispetto alla circonferenza

E’ noto che una retta è esterna ad una circonferenza se non ha alcun punto in comune con essa. E’ secante se ha due punti distinti in comune, è tangente se ha 1 solo punto in comune con essa.

Nel primo caso la distanza della retta dal punto C, cioè il centro, è maggiore del raggio. Nel secondo caso è minore del raggio, nel terzo caso sono invece coincidenti.

Per determinare gli eventuali punti di intersezione con una retta bisogna risolvere il sistema di equazioni di secondo grado formato da:

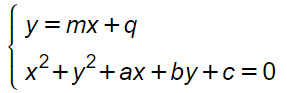
Tale sistema si risolve in genere per sostituzione. Abbiamo tuttavia dedicato una lezione specifica per l’argomento piena di esercizi svolti e con tutti casi possibili che possono esserci nei compiti in classe.

Approfondimento: Retta tangente alla circonferenza

Di seguito trovi tutte le lezioni dedicate allo studio della circonferenza nel piano cartesiano.

Elenco delle lezioni