Equazioni goniometriche – lo schema per risolverle facilmente

Le equazioni goniometriche sono delle equazioni in cui l’incognita compare come argomento delle funzioni goniometriche (seno, coseno, tangente, cotangente). Esistono vari metodi per risolverle a seconda della tipologia. Vedremo in questa lezione come si risolvono le equazioni goniometriche, con esercizi svolti ed esempi commentati caso per caso.

Prima di vedere quali sono i tipi di equazioni goniometriche che possiamo trovare negli esercizi, cerchiamo di dare una definizione matematica.

Cosa sono le equazioni goniometriche

Si dice equazione goniometrica quella in cui l’incognita x compare come argomento di una o più funzioni trigonometriche. Vediamo subito un facile esempio:

• senx=1/2
• senx+cosx=1
• x cosx-1=0
• x-tgx=0

Come puoi vedere la x compare proprio all’interno di seno, coseno, tangente e cotangente, per cui i metodi che abbiamo fino ad ora studiato per risolvere le equazioni e disequazioni vanno ampliati. Per risolvere le equazioni goniometriche è necessario trovare quegli angoli che verificano l’uguaglianza tra i due membri dell’equazione stessa.

Ci hai capito poco vero? Non preoccuparti, tra poco ti sarà tutto più chiaro. Iniziamo proprio vedendo qual è il caso base più semplice che è possibile trovare.

Equazioni gioniometriche elementari

Prima di partire con le espressioni goniometriche più difficili, vediamo la forma base, la più semplice in assoluto. Il nostro obiettivo sarà, in tutti gli esercizi, cercare di ricondurci a una di queste 4 forme.

senx=m

cosx=n

tgx=p

cotgx=q

Queste quattro che ti abbiamo elencato vengono dette equazioni goniometriche elementari. Analizziamo ora singolarmente i vari casi e per ciascuna vedremo i metodi di risoluzione. Ecco una tabella molto schematica che ti aiuterà a comprendere meglio l’argomento.

• senx=m

Per risolvere questa prima equazione goniometrica è necessario che -1<=m<=1 (cioè m deve essere compreso o uguale da -1 e +1). In maniera molto semplice l’esercizio ti chiede di trovare quell’angolo x il cui valore del seno è pari a m. Poiché i valori del seno si ripetono ogni 360 gradi, allora possiamo dire che la soluzione sarà valida per ogni 2kπ.

x=a+2kπ

• cosx=n

Anche in questo caso per risolvere l’equazione goniometrica è necessario che -1<=n<=1 (cioè n deve essere compreso o uguale a -1 e +1).  In caso contrario l’equazione è impossibile. L’esercizio ci chiede di trovare il valore di quell’angolo il cui coseno è pari a n. Vale (per i 2kπ) quanto già detto con le equazioni con il seno.
x=a+2kπ

• tgx=p

La condizione di esistenza, affinché l’equazione non sia impossibile, è che x deve essere diverso da 90° (cioè π/2 espresso in radianti). Per risolvere le equazioni elementari con la tangente è necessario trovare quell’angolo la cui tangente è pari a p. Poiché la tgx è una funzione periodica – cioè che si ripete – ogni 180°, allora il risultato sarà valido per ogni kπ.
x=a+kπ

• cotgx=q

Deve valere la condizione x diverso da kπ. E’ necessario ora trovare quell’angolo x la cui cotangente è proprio q. Vale lo stesso discorso della periodicità della tangente, per cui anche le equazioni con la cotangente sono valide ogni kπ.
x=a+kπ

Esempi sulle equazioni goniometriche elementari

ESERCIZIO 1

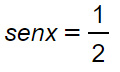
Eccome come ragionare per risolvere le equazioni goniometriche: l’esercizio mi chiede qual è quel valore dell’angolo per cui il seno vale 1/2. Poiché il seno di 30° e il seno di 150° sono uguali a 1/2, allora possiamo scrivere:

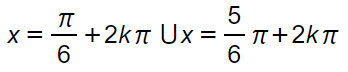
ESERCIZIO 2

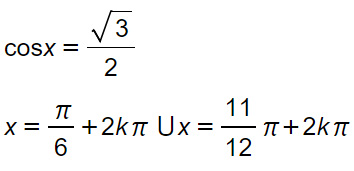
In questo secondo esercizio la traccia sostanzialmente ci ha chiesto: qual è quel valore dell’angolo x per cui il coseno vale radical 3 fratto 2? Ricordando che il coseno di 30 gradi e di 330 gradi valgono proprio radical 3 fratto 2, allora si arriva alla soluzione in un unico passaggio.

Regola generale per risolvere le equazioni goniometriche

Ogni volta che ti trovi di fronte ad un’equazione goniometrica elementare, poniti la domanda: che angolo devo trovare affinché la funzione trigonometrica mi restituisca quel valore? Disegna (se necessario) la circonferenza goniometrica, oppure stampa le nostre tabelle sui valori di seno e coseno.

Ecco altri 2 esempi svolti con la soluzione, ti trovi con il risultato?

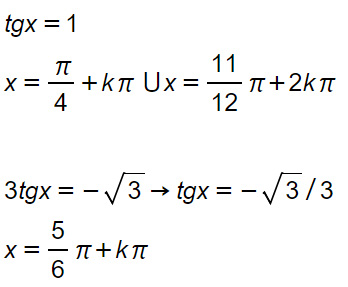
Equazioni goniometriche riconducibili ad elementari

Alcune equazioni pur essendo non elementari, possono considerarsi riconducibili alla prima tipologia che abbiamo visto. A volte è sufficiente eseguire qualche passaggio algebrico, a volte se si presentano più funzioni goniometriche è possibile esprimerle attraverso una sola di esse (riguardati le relazioni generali della trigonometria), altre volte è possibile applicare le formule degli archi associati.

Chiariamo questo concetto con degli esercizi svolti:

Come puoi vedere i primi passaggi sono determinanti. Avendo una funzione al quadrato, vuol dire che l’equazione non è elementare. Posso però applicare la regola della moltiplicazione di una somma per una differenza. Successivamente applicando la regola dell’annullamento del prodotto si arriva facilmente alla soluzione. Prova a guardare ora quest’altro esercizio svolto:

In quest’ultimo esempio i metodi di risoluzione erano due: noi abbiamo preso la strada più breve cioè usando la scomposizione del quadrato di binomio. In realtà si poteva scomporre quest’equazione trinomia con il metodo del delta che hai imparato con le equazioni di secondo grado. Questo esercizio svolto infatti altro non era che un’equazione goniometrica riconducibile a elementare di secondo grado. Per risolverla sono semplicemente necessarie opportune scomposizioni iniziali.

Riconducibili ad elementari con le formule goniometriche

Alcune equazioni goniometriche possono essere ridotte ad elementari, attraverso l’applicazione di opportune formule di addizione o sottrazione, oppure con le formule di duplicazione o bisezione, prostaferesi o Werner. Cerchiamo subito di chiarire questo concetto con 2 esempi:

In questo primo esempio abbiamo semplicemente applicato la formula di addizione, risolto pochi facili passaggi algebrici per arrivare alle equazioni goniometriche elementari rapidamente e quindi alla soluzione. Niente di particolarmente complesso, per cui vediamo un altro esercizio svolto…

L’ultimo esempio fa parte delle equazioni goniometriche con le formule di Prostaferesi (se non le ricordi ecco un file doc per poterle rivedere). Solo così possiamo da moltiplicazione a somma con le funzioni trigonometriche e ottenere la soluzione.

Equazioni goniometriche lineari

Un equazione lineare in seno e coseno si presenta nella forma a senx + b cosx = c. Distinguiamo ora due casi:

• c=0

allora conviene dividere tutta l’equazione per cosx ottenendo:

a senx/cosx + b cosx/cosx = 0
a tgx + b = 0
tgx=-b/a

ossia un’equazione elementare.

• c diverso da zero

In questo caso ci sono due metodi di risoluzione altrettanto validi. Il primo consiste nel risolvere le equazioni goniometriche con le formule parametriche. E’ il metodo più veloce e semplice (se ricordi le formule) per cui te lo consigliamo. Ecco degli esercizi svolti sulle equazioni goniometriche parametriche:

Il secondo che ti stiamo presentare è il metodo grafico per le equazioni goniometriche lineari. Data l’equazione generica asenx+bcosx=c, possiamo porre  senx=X e cosx=Y. Ricordando la relazione fondamentale della trigonometria (seno al quadrato più coseno al quadrato uguale a 1), possiamo scrivere il seguente sistema:

Sostanzialmente le due figure che si generano l’equazione di una retta e di una circonferenza. Dalla loro intersezione, quindi risolvendo il sistema indicato (se non ricordi come fare riguardati la nostra lezione sui sistemi di equazioni), otterrai le soluzioni dell’equazione lineare. Vediamo un esempio:

Equazioni goniometriche omogenee

Le equazioni che si presentano nella forma:

si dicono omogenee di 2 grado in seno e coseno, perché tutti i termini sono di secondo grado. Per risolvere le equazioni omogenee in trigonometria si divide tutto per il coseno al quadrato (supposto che cosx=0 non è una soluzione del sistema, cioè effettuate le dovute condizioni di esistenza). In questo modo si esprime tutto in funzione della tangente. Vediamo subito un esempio:

La prima cosa da fare è chiederci: cosx=0 può essere una soluzione? Poiché per cosx=0, x=90°+2k180°, basta che vado ad inserire 90° nell’equazione. Se esce 0 allora anche la x che abbiamo verificato è una soluzione. Possiamo ora affrontare il calcolo:

Sono perfettamente identiche le equazioni trigonometriche riconducibili ad omogenee. L’unica differenza è che dovrai ingegnarti all’inizio con alcuni passaggi algebrici per poterti ridurre alla condizione di equazione omogenea.

Per evitare di appesantire la lezione, ti invitiamo ora a fare soltanto degli esercizi (a questo link trovi tutti gli esercizi sulle equazioni goniometriche). Nella prossima lezione vedremo i sistemi di equazioni goniometriche.