Equazioni esponenziali – esercizi svolti e commentati

In una precedente lezione avevamo visto la spiegazione completa sulle equazioni esponenziali. Nella lezione svolgeremo assieme un’esercitazione cercando di mettere in pratica quello imparato nella parte teorica.

Approfondiremo quindi le equazioni esponenziali con esercizi svolti e commentati passo passo, dai casi più semplici – equazioni elementari – a quelli più complessi con i logaritmi o i sistemi.

Esercizi svolti ed esempi

Ti ricordiamo che per la risoluzione di questa esercitazione è importante avere confidenza con le proprietà delle potenze e con le regole sui logaritmi. Senza dilungarci in troppe chiacchiere vediamo subito il primo esercizio svolto.

Esercizio 1

Risolvere le equazioni esponenziali seguenti:

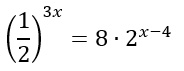
La prima cosa che possiamo notare è che quasi tutti i numeri presenti alle basi possono essere riscritti come una potenza a base 2. Anche 1/2, ricordando la proprietà delle potenze negative.

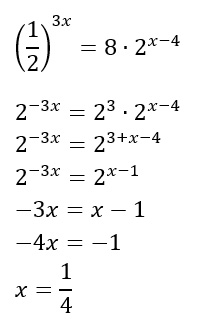
Come puoi vedere in questo primo esempio svolto, la prima cosa da fare è cercare di capire se siamo in presenza di un’equazione esponenziale con le stesse basi. In questo caso l’esercizio diventa molto più facile: solo ricordando le regole e gli esercizi svolti sulle potenze (in particolare sulle potenze negative) siamo riusciti a passare da 1/2 a 2 semplicemente mettendo un segno meno all’esponente. Il resto del problema non è difficile, si tratta di semplici passaggi algebrici.

Esercizio 2

In questo secondo problema appare subito evidente che la base non è la stessa: si tratta di un’esercizio con equazione esponenziale con basi diverse per cui dovremo necessariamente usare i logaritmi. Ci sono due modi di procedere: usare i logaritmi naturali (cioè con il numero di Nepero) o decimali, oppure usare la stessa base degli esponenziali, che è la strada che noi preferiamo. Vediamo come si risolve:

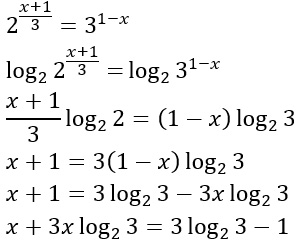
Nell’ultimo passaggio, così come visto per le equazioni di primo grado, portiamo i termini con l’incognita x a sinistra mentre i numeri, cioè i termini noti, vanno a destra. Effettuiamo ora il raccoglimento a fattor comune della x e l’esercizio è svolto.

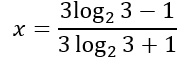
Esercizio 3

Risolvere l’equazione esponenziale seguente:

Ti ricordi che hai già incontrato in passato le equazioni biquadratiche? Lo svolgimento è del tutto analogo. Facciamo una sostituzione per semplificarci la risoluzione dell’esercizio: t è uguale 2 elevato a x.

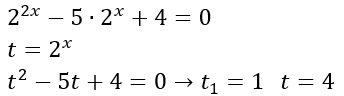
Abbiamo cioè trovato un’equazione di secondo grado da risolvere in pochi semplici passaggi con il metodo del delta. In questo modo troviamo due soluzioni, cioè t1 e t2. Non dimentichiamoci di riapplicare la sostituzione iniziale per concludere l’esercizio.

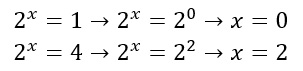
Esercizio 4

L’ultimo esempio che ti mostriamo, infine, riguarda i sistemi di equazioni esponenziali, in cui compaiono cioè 2 incognite.

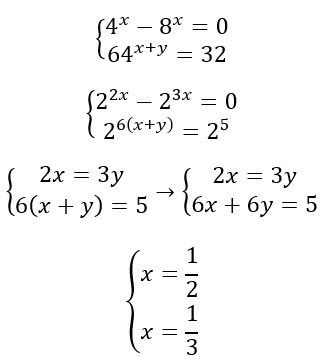
In questo tipo di esercizio non c’è nulla di particolarmente difficile. Abbiamo risolto e semplificato le equazioni in maniera indipendente e poi usato la regola dei sistemi di equazioni – come il metodo di sostituzione. La regola non sarebbe cambiata se ci fossero state 3 incognite e quindi tre equazioni esponenziali da risolvere.

Esercizio 5

Il prossimo esercizio è molto più semplice di quel che si creda. Infatti non può essere considerata una vera e propria equazione esponenziale fratta, ma non bisogna comunque dimenticarci di porre le condizioni di esistenza.

Essendoci una frazione, occorre cioè porre il denominatore diverso da zero. Cioè 4 elevato a 2x-5 diverso da 0. Poiché la funzione esponenziale è sempre positiva, allora il risultato è sempre maggiore di zero.

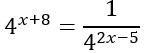
Aggiungiamo un meno all’esponente del secondo membro, così da portare tutto al numeratore.

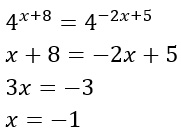
Altri esercizi in pdf e conclusioni

Dopo aver visto degli esempi svolti ed esercizi con soluzione, prova ora ad esercitarti da solo. Troverai tante tracce interessanti a questo PDF. C’è un’interessante raccolta di esercizi: prova a risolverli tutti! Solo così puoi fare una verifica di quanto hai realmente appreso in questa lezione.