Le equazioni esponenziali (così come le disequazioni esponenziali), contengono almeno una potenza con l’incognita nell’esponente. Vediamo la forma più semplice:
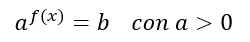
Ti starai chiedendo: come si fanno le equazioni esponenziali? Considerando la forma scritta sopra, è possibile risolverla in modo immediato se si riescono a scrivere a e b come potenze aventi la stessa base.
Vedremo però anche altri modi di risoluzione, sfruttando ad esempio le proprietà delle potenze e le proprietà dei logaritmi.
Come riconoscerle
E’ semplicissimo: se all’esponente trovi l’incognita x allora si tratta di una equazione con esponenziale. Nei prossimi due esempi, noterai che la seconda è una semplice equazione di primo grado.
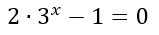
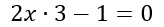
Equazioni esponenziali schema
Risolvere le equazioni esponenziali è semplice, tutto sta nel ricondurre la nostra equazione alla forma normale. Quelle che vedi di seguito vengono anche chiamate equazioni esponenziali elementari.
Forma elementare
(di TIPO 1)
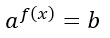
Doppio esponenziale
(di TIPO 2)
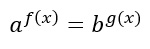
Analizziamo più nel dettaglio come risolvere entrambe le forme.
Come si risolvono le equazioni esponenziali di tipo 1?
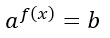
L’equazione si risolve in modo immediato se a e b possono essere scritti come potenze con la stessa base. Ad esempio:
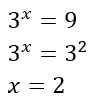
Come hai visto il termine b è stato scritto come una potenza facendo in modo che abbia la base proprio pari ad a. Infine sono stati eguagliati gli esponenti.
Equazioni esponenziali con logaritmi
Nel caso in cui non sia possibile ridurre il termine noto a una potenza con la stessa base di a, allora è necessario ricorrere ai logaritmi.
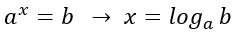
Come si arriva a quel risultato? In maniera molto semplice applichiamo il logaritmo a destra e sinistra dell’uguale.
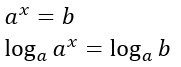
Come hai potuto notare ho applicato il logaritmo in base a, vedremo che ci semplifica tutti i calcoli. A questo punto è sufficiente applicare le proprietà dei logaritmi (se non le ricordi questo articolo fa al caso tuo 😉 ).
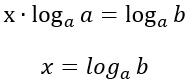
NB: questo metodo può essere applicato anche nel caso in cui a e b possono essere scritti come potenze con la stessa base!
Casi particolari
- Per b ≤ 0 → poiché la funzione esponenziale è sempre positiva il risultato dell’equazione esponenziale è IMPOSSIBILE;
- Per a=1 e b≠1 → è il secondo caso per cui il risultato è IMPOSSIBILE;
- Per a=1 e b=1→ l’equazione è INDETERMINATA
Come risolvere le equazioni esponenziali di tipo 2?
Anche in questo caso possiamo distinguere due casi:
- Equazioni esponenziali con la stessa base
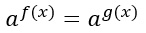
In questo caso mi trovo in un caso elementare poiché le due basi sono uguali e quindi basta uguagliare le basi. La mia soluzione è data da
f(x) = g(x).
- Equazioni esponenziali con base diversa
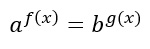
Innanzitutto provo a scrivere b come potenza di a, così da ricondurre entrambi i membri ad una stessa base. Se questo è possibile, mi trovo nel caso precedentemente spiegato:
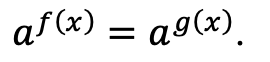
Se invece non è possibile, ricorro alle regole dei logaritmi. Pertanto, così come visto nelle equazioni di tipo 1, avrò:
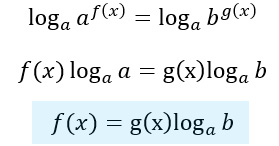
Come risolvere le equazioni esponenziali fratte
E se la nostra equazione ha l’incognita al denominatore? Nessuna paura!
L’equazione si risolve con i metodi che abbiamo visto precedentemente, facendo però attenzione alle condizioni di esistenza. Infatti, poiché l’incognita si trova al denominatore, bisogna porre quest’ultimo diverso da 0. Vuoi capirne di più? Vedi gli esercizi svolti di seguito!
Esercizi svolti ed esempi
Ora che la teoria è finita… facciamo un po’ di pratica!
Di seguito troverai diversi esercizi svolti e commentati passo passo che coprono la maggior parte delle tipologie che puoi incontrare.
Partiamo da quelli più semplici fino ad arrivare a quelli più complessi 🙂
1) Come risolvere le equazioni esponenziali elementari con le potenze
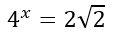
In questo caso non c’è nessuna condizione di esistenza da imporre poiché
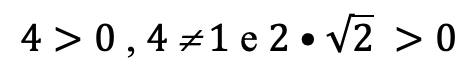
Non rientriamo quindi nei casi particolari che abbiamo visto. La prima cosa da verificare è capire se si può portare entrambi i membri ad una stessa base.
Applicando le proprietà delle potenze abbiamo che 4 = 2 • 2 , inoltre otteniamo:
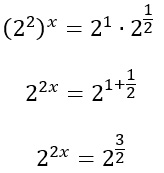
Ora che entrami i membri hanno la stessa base, per trovare l’incognita x basterà uguagliare:
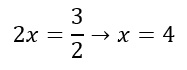
2) Esempio di equazione esponenziale impossibile
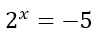
L’equazione non è verificata per nessun valore reale di x, infatti le condizioni di esistenza non sono soddisfatte, visto che b è minore di 0. Pertanto il risultato è IMPOSSIBILE.
3) Come risolvo equazioni esponenziali con i logaritmi
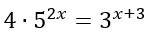
Entrambi i membri dell’equazione sono numeri positivi e, poiché non è possibile ricondurre a e b ad una stessa base, applichiamo le regole dei logaritmi.
Applichiamo il logaritmo in base 10 ad entrambi i membri:
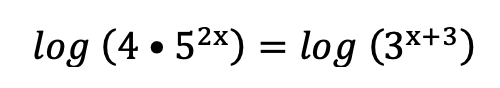
NB: per semplicità abbiamo applicato il log in base 10 ma possiamo usarlo in una base qualsiasi, compreso il numero di Nepero e, purché sia la stessa ad entrambi i membri!
Applicando le regole dei logaritmi:
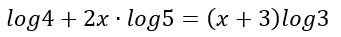
Eseguo un raccoglimento a fattor comune. Raccolgo cioè la x:
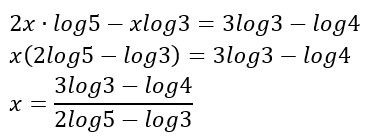
4) Come risolvere le equazioni esponenziali con base diversa
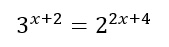
Applichiamo ad entrambi i membri il logaritmo in base 10 (sottinteso):
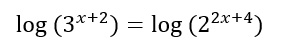
Usando le regole dei logaritmi otteniamo:
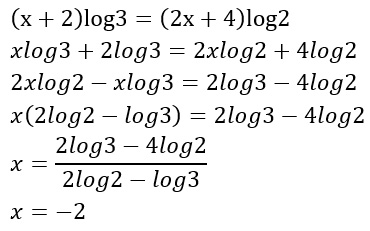
5) Come risolvere le equazioni esponenziali fratte
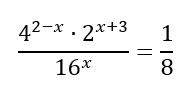
Entriamo nella categoria degli esercizi un po’ più difficili. Dato che abbiamo l’incognita al denominatore, dobbiamo imporre le condizioni di esistenza:
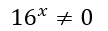
Come possiamo notare, la diseguaglianza è sempre verificata a prescindere dal valore dell’incognita x poiché 16 > 0 e quindi 16 elevato ad x è sempre > 0 per ogni x in ℝ.
Tornando alla risoluzione dell’equazione, utilizziamo le proprietà delle potenze per far sì che i termini abbiano la stessa base.
Al numeratore abbiamo:
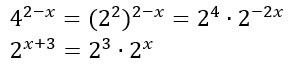
Al denominatore abbiamo:
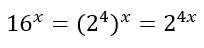
Al secondo membro abbiamo:
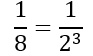
Riscriviamo quindi l’equazione come segue:
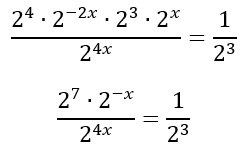
Applichiamo la proprietà del quoziente per potenze con la stessa base e la regola delle potenze negative:
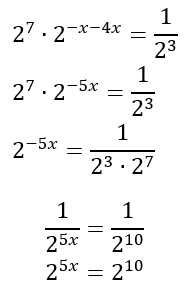
Ora che le basi sono le stesse, possiamo imporre l’uguaglianza tra gli esponenti:
5x=10
x=2
Conclusioni
Per affrontare al meglio le equazioni esponenziali è bene avere chiare le proprietà sulle potenze e le proprietà dei logaritmi. Risulteranno infatti fondamentali nella risoluzione degli esercizi!
Come abbiamo visto lo svolgimento è molto semplice, dobbiamo però fare attenzione a ricondurci alla forma normale (cioè quella più semplice) corretta.
Se hai voglia di metterti alla prova con ulteriori esercizi, dai un’occhiata all’esercitazione: esercizi equazioni esponenziali!
Se hai ulteriori dubbi o se l’articolo ti è stato utile, lascia un commento! Saremo lieti di aiutarti 🙂