In questo primo capitolo ci occuperemo di una delle prime tipologie di equazioni differenziali che si studiano nei programmi di analisi: le equazioni lineari del primo ordine. Partiremo dalla definizione e dalla forma normale, vedremo le formule usate per la loro risoluzione e completeremo il tutto con degli esercizi svolti e commentati.
Ti ricordiamo che per risolvere le equazioni differenziali è necessario avere piena padronanza delle tecniche di risoluzione degli integrali. Vedremo infatti che la formula risolutiva si riduce a un semplice integrale con una funzione esponenziale all’interno.
In questa lezione vedremo come si risolvono le equazioni differenziali lineari del primo ordine, vedremo nelle lezioni successive come si risolvono le non lineari o quelle del secondo ordine. Partiamo ora subito cercando di capire che cos’è un’equazione differenziale lineare del primo ordine.
Definizione
Un’equazione differenziale si dice lineare quando si presenta nella forma:
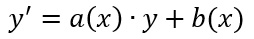
dove y è la funzione incognita e a(x) e b(x) sono due funzioni di x continue in un certo intervallo I. La soluzione di questo particolare tipo di equazione è una funzione derivabile in I, che soddisfa l’equazione per ogni x appartenente ad I. Per risolvere queste equazioni differenziali vale la seguente formula/teorema.
TEOREMA (formula risolutiva)
Integrale generale di un’equazione differenziale lineare del primo ordine
L’integrale generale dell’equazione y’=a(x)y+b(x) si determina attraverso la formula:
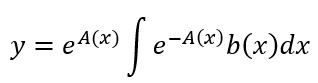
dove A(x) è la primitiva della funzione a(x). Nel caso particolare in cui b(x) sia una funzione costante e pari a 0, l’equazione si dice omogenea e il suo integrale generale si semplifica per diventare:
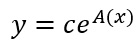
Detto in parole povere
Quando devi risolvere un’equazione differenziale lineare del primo ordine ecco come procedere:
- individua subito le funzioni a(x) e b(x);
- calcola A(x), ovvero calcola l’integrale indefinito della funzione a(x);
- applica la formula risolutiva.
Equazioni differenziali lineari esercizi svolti
ESERCIZIO 1
Risoluzione di un’equazione differenziale lineare del primo ordine.
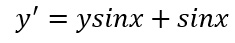
Passo 1 – Identifichiamo subito le funzioni a(x) e b(x). Confrontandolo con la forma normale y’=a(x)y+b(x), capiamo immediatamente che a(x)=sinx e b(x)=sinx
Passo 2 – Calcoliamo A(x) facendo l’integrale di a(x), ovvero l’integrale della funzione seno.
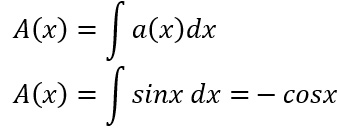
Passo 3 – Scriviamo l’integrale generale servendoci della formula risolutiva vista prima.
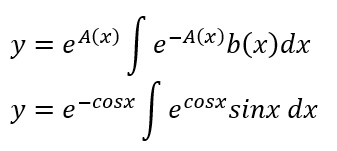
A questo punto non ci resta che risolvere l’integrale esponenziale. Notiamo che si presenta nella forma e elevato a f(x) ed è già moltiplicato per f'(x), visto che il seno è la derivata del coseno (a meno di un segno!!). Aggiungiamo quindi un segno meno così che sia presente preciso f'(x) e risolviamo:
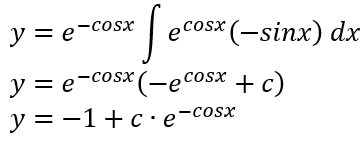
Attenzione alla costante c
Non dimenticare mai la costante d’integrazione c: è fondamentale per esprimere l’integrale generale (ovvero la soluzione generale) delle equazioni differenziali lineari di primo ordine. Sarà altrettanto importante per risolvere i problemi di Cauchy ed ottenere gli integrali particolari (ovvero la soluzione particolare), in cui bisognerà proprio determinare il valore di tale costante.
ESERCIZIO 2
Risolvere l’equazione differenziale lineare del primo ordine:
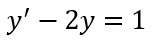
Si tratta di un esercizio molto semplice che risolveremo in pochi semplici passaggi. Trasformiamo l’equazione isolando il termine y’ a sinistra e portando tutto il resto a destra:
y’=2y+1
Possiamo riconoscere facilmente le due funzioni a(x) e b(x) in questo caso entrambe costanti. In particolar modo a(x)=2 e b(x)=1. Calcoliamo quindi il valore di A(x) facendo l’integrale di a(x), ovvero l’integrale di 2, pari proprio a 2x. Quindi la soluzione si scrive usando la formula:
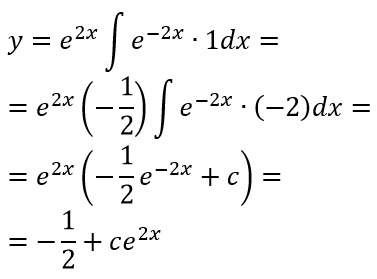
ESERCIZIO 3
Proviamo a risolvere l’equazione differenziale lineare di primo ordine:
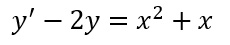
Confrontiamo la traccia con la y=a(x)y+b(x):
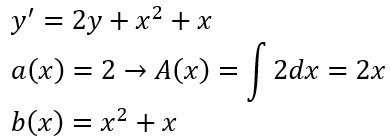
A questo punto possiamo utilizzare la formula vista prima e svolgere gli integrali per parti:
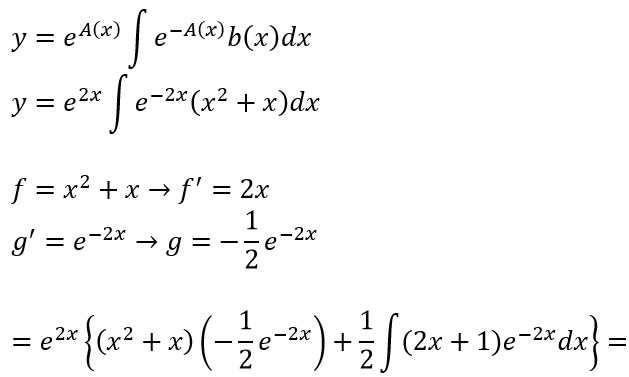
Proseguiamo lo svolgimento dell’ultimo integrale procedendo ancora per parti:
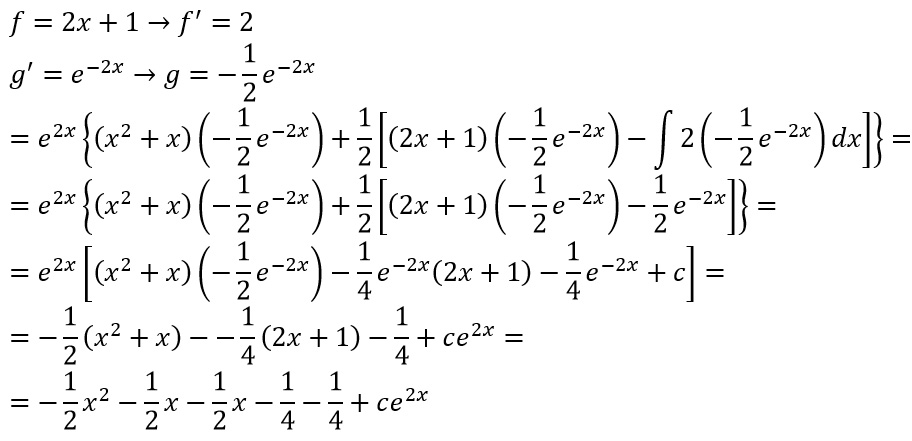
Possiamo così concludere questo esercizio scrivendo la soluzione dell’equazione differenziale lineare:
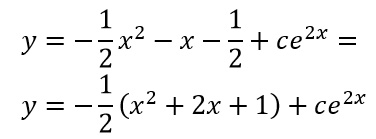
La prossima lezione: Equazioni differenziali a variabili separabili
Conclusioni
Abbiamo visto che la risoluzione delle equazioni differenziali di primo ordine lineari si traduce in un integrale con un esponenziale e, negli esercizi più complessi, sarà sufficiente provare a risolvere per parti.
Se hai trovato questa lezione chiara o se hai ancora dei dubbi, lascia un commento/feedback in basso. Il nostro staff ti risponderà nel minor tempo possibile.