In questa lezione vedremo in maniera semplice ma efficace come risolvere le equazioni differenziali a variabili separabili, andando ad analizzare i metodi più veloci per arrivare ad ottenere la soluzione (detta anche integrale) generale o particolare.
Definizione
Un’equazione differenziale del primo ordine si dice a variabili separabili quando la derivata prima delle funzione incognita (y’) può scriversi come il prodotto di una funzione della sola variabile indipendente x e di una funzione della sola variabile y.
Dal punto di vista matematico, un’equazione differenziale a variabili separabili può essere scritta con la seguente formula:
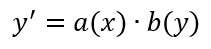
dove a(x) e b(y) sono due funzioni continue.
In parole povere, all’interno dell’equazione devono essere facilmente riconoscibili due blocchi tra loro moltiplicati, il primo può contenere come variabile solo la x, mentre il secondo può avere come variabile solo la y.
Come riconoscere le equazioni differenziali a variabili separabili
ESEMPIO 1
Proviamo a fare qualche piccolo esempio per capire meglio come sono fatte queste particolari equazioni differenziali di primo ordine.
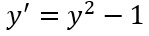
E’ un’equazione differenziale a variabili separabili? SI, perché al secondo membro abbiamo una funzione “y al quadrato meno uno” che è funzione solo della y. Manca la x? Non c’è problema perché possiamo anche riscrivere la traccia come:
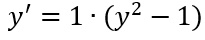
Quel termine 1 che abbiamo aggiunto con la moltiplicazione, è proprio la nostra a(x), ovvero la funzione che dipende solo da x. In questo caso è come se avessimo x elevato a 0 (ogni numero elevato a 0 fa 1)
ESEMPIO 2
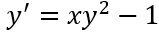
E’ un’equazione differenziale a variabili separabili? NO, perché in questo caso abbiamo una funzione in cui le variabili x e y non possono essere separate. Infatti non possiamo riconoscere direttamente un a(x) e un b(x) anche a causa di quel -1 finale.
Come risolvere le equazioni differenziali a variabili separabili
Per determinare la soluzione, che in linguaggio matematico viene indicata anche come integrale generale, si procede con due semplici passaggi:
- Si risolve b(y)=0. Il valore di y che ottieni sarà una prima soluzione dell’equazione differenziale.
- Supposto b(y) diverso da 0, allora nella nostra traccia, al posto di y’, andremo a scrivere la derivata con la notazione di Liebniz:
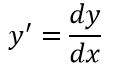
Così da poter riscrivere la traccia come:
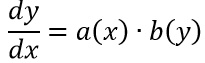
A questo punto, attraverso semplici passaggi algebrici, possiamo spostare dx al secondo membro, proprio accanto a a(x). Contemporaneamente b(y) passa al primo membro accanto a dy. Siamo pronti così per applicare l’integrale.
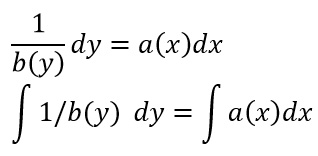
Non resta che risolvere i due integrali nel metodo che si ritiene più opportuno individuando le primitive A(x) e B(x) rispettivamente di a(x) e 1/b(y), aggiungendo la costante di integrazione c.
Equazioni differenziali a variabili separabili esercizi svolti
Proviamo a mettere in pratica il metodo appena visto analizzando alcuni esercizi e commentando ogni singolo passo.
Esercizio 1
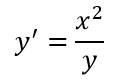
Il primo passo è quello di riconoscere il tipo di equazione differenziale da risolvere. In questo caso possiamo riscrivere la traccia nella forma più semplice:
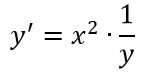
In questo modo possiamo riconoscere immediatamente le due funzioni di x e di y: a(x) e b(y).
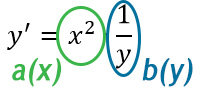
Come visto nella parte teorica, iniziamo cercando la soluzione più semplice imponendo b(y)=0, cioè 1/y=0, che da come risultato impossibile. Per cui possiamo proseguire utilizzando la notazione di Liebniz:
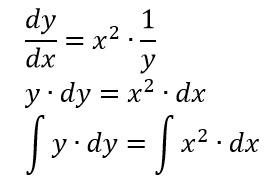
Una volta applicati gli integrali, possiamo risolvere, per ottenere quindi:
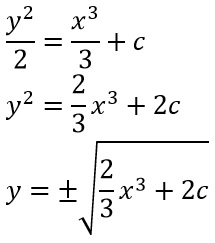
Abbiamo quindi determinato il valore di y, cioè il valore dell’integrale generale. Da notare che al secondo membro c’è quel 2c, che non è altro che una costante, che quindi possiamo più semplicemente esprimere come c o in alcuni testi, per non generare confusione viene chiamata c1.
Esercizio 2
Aumentiamo leggermente il grado di complessità dell’esercizio.
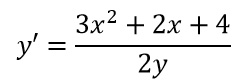
Prima operazione: riconoscere il tipo di equazione differenziale. Anche in questo caso possiamo riscriverci la traccia isolando due funzioni differenti, una con la sola variabile x e una con la sola y.
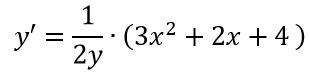
Proviamo subito la soluzione immediata imponendo b(y)=0, cioè 1/2y=0. Poiché si tratta di un’equazione fratta, risolviamo imponendo numeratore uguale a 0 e denominatore diverso da 0. Il risultato è impossibile (perché 1 non è mai uguale a 0). A questo punto usiamo la notazione di Liebniz e separiamo le variabili nei due membri dell’equazione:
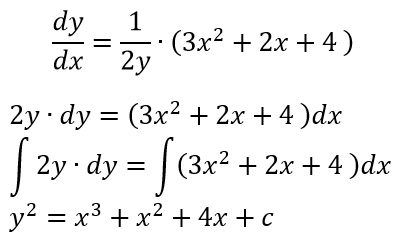
Dopo aver applicato l’integrale a primo e secondo membro, abbiamo così ottenuto la soluzione implicita del nostro problema. Possiamo esplicitare la y semplicemente applicando una radice quadrata ai due membri dell’equazione.
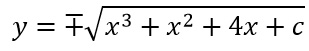
Esercizio 3
Chiudiamo gli appunti di questa lezione applicando quello appreso fino a questo momento al problema di Cauchy. Che cos’è? Non è altro che un’equazione differenziale del primo ordine (nel nostro caso, ma può essere anche di ordini superiori) in cui bisogna andare a calcolare il valore della costante c grazie a delle condizioni date dal problema.
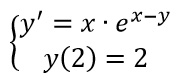
Possiamo sfruttare le proprietà delle potenze per riscrivere la traccia e trovare le due funzioni a(x) e b(y).
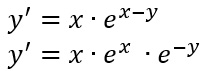
La soluzione immediata è b(y)=0, ovvero e elevato alla meno y uguale a 0, che è impossibile visto che una funzione esponenziale non può essere mai uguale a 0. Allora procediamo con la notazione di Liebniz:
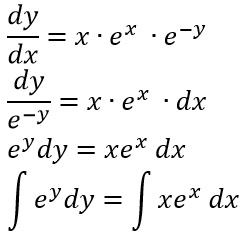
A questo punto, mentre il primo è di immediata risoluzione, possiamo risolvere il secondo integrale ricorrendo alla regola di integrazione per parti. Per cui otteniamo:
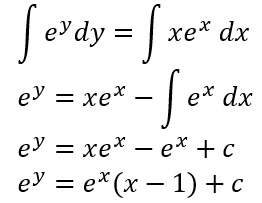
Come puoi vedere, subito dopo aver effettuato il raccoglimento a fattor comune di e alla x, siamo arrivati alla soluzione implicita del problema. Possiamo ottenere quindi la soluzione esplicita applicando il logaritmo naturale ad ambo i membri dell’equazione.
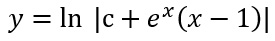
A questo punto possiamo inserire la condizione dettata dal problema di Cauchy nella soluzione implicita trovata. Cioè, poiché y(2)=2, inserisco 2 al posto della x e della y. Ottengo quindi:
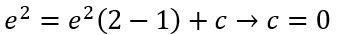
Sostituiamo c=0 nella soluzione esplicita individuata e abbiamo terminato:
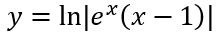
Conclusioni
Abbiamo visto in questa lezione quanto sia semplice risolvere le equazioni differenziali a variabili separabili. L’unica vera difficoltà sta nel riconoscere dalla traccia le due funzioni a(x) e b(y) e se quindi sia effettivamente un’equazione differenziale a variabili separabili. Il nostro consiglio è di procedere, se necessario, con qualche piccola manipolazione algebrica, proprio come abbiamo fatto negli ultimi due esercizi.
Se questa lezione ti è stata utile, lasciaci un commento. Un tuo feedback positivo ci aiuterà a migliorare la qualità delle nostre lezioni e ad offrirti sempre più esercizi commentati e svolti. Buono studio!