Le disequazioni logaritmiche sono delle disequazioni in cui l’incognita compare come argomento del logaritmo.
In questa lezione vedremo che cosa sono e come si risolvono le disequazioni logaritmiche attraverso una breve spiegazione teorica e numerosi esercizi svolti da usare come esempio.
Per poterlo fare è necessario conoscere bene quali sono le proprietà dei logaritmi, dal cambio di base alla trasformazione in esponenziali.
Che cos’è una disequazione logaritmica?
Nell’introduzione l’abbiamo già definita come una disequazione che ha l’incognita x all’interno dell’argomento del logaritmo. Ecco un esempio:
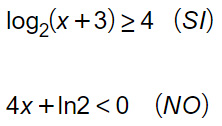
Dei due esempi sopra, si nota come la prima rientri tra le disequazioni logaritmiche. La seconda invece no perché appartiene alle più semplici disequazioni di primo grado, visto che l’incognita x non è nell’argomento del logaritmo.
Risolvere disequazioni logaritmiche
Ti ricordi come si risolvono le equazioni logaritmiche? Il ragionamento è molto simile: ci sono delle condizioni di esistenza da sviluppare parallelamente all’esercizio principale.
La differenza è che con le disequazioni logaritmiche abbiamo un sistema di disequazioni da risolvere. La prima disequazione è quella principale dell’esercizio, mentre tutte le altre sono date dalle condizioni di esistenza dei vari logaritmi.
Come si risolvono le disequazioni logaritmiche
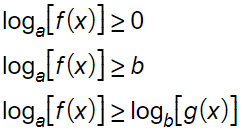
Le tre disequazioni possono apparire con il simbolo maggiore, minore, maggiore e uguale o minore e uguale. Queste rappresentano sostanzialmente i tre tipi di disequazioni con i logaritmi che si possono dover svolgere in esercizi o compiti.
Ricordando che la condizione di esistenza del logaritmo impone di scrivere che l’argomento maggiore di 0, allora possiamo risolvere le disequazioni logaritmiche scrivendo un sistema di disequazioni:
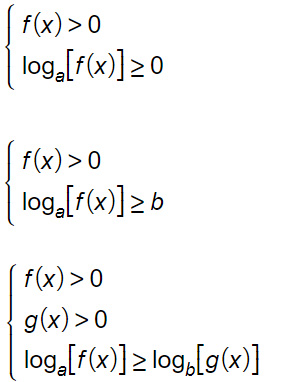
Per ogni rigo si scriverà la condizione di esistenza di ogni logaritmo, mentre all’ultimo rigo si riscrive la disequazione logaritmica della traccia. Vediamo questi tre casi come si risolvono singolarmente.
Disequazione logaritmica di tipo 1
Abbiamo una disequazione con un logaritmo che ha al secondo membro lo 0.
![]()
Abbiamo visto che questa disequazione si risolve scrivendo il sistema in cui sono incluse le condizioni di esistenza f(x)>0.
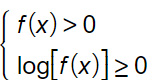
Mentre la prima si risolve come una normale disequazione, resta da capire come risolvere la seconda. Sfruttiamo la proprietà dei logaritmi: il logaritmo di 1 è sempre uguale a 0.
ATTENZIONE: non confonderti con il logaritmo di 0 che invece non esiste!
Per cui possiamo trasformare lo 0 nel logaritmo con la stessa base:
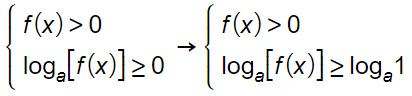
A questo punto, visto che nella disequazione logaritmica ci sono le stesse basi, possiamo considerare solo gli argomenti e togliere i logaritmi.
Con equazioni e disequazioni logaritmiche bisogna distinguere due casi a seconda della base del logaritmo.
- a>1 : la base del logaritmo è maggiore di 1, la disequazione con i logaritmi può essere riscritta senza alcuna variazione.
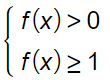
- 0<a<1 : la base del logaritmo è compresa tra 0 e 1. Si va a modificare il verso della disequazione con i logaritmi. Se c’è maggiore (o maggiore e uguale) si mette minore (o minore e uguale) e viceversa.
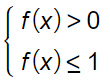
Disequazione logaritmica di tipo 2
Vediamo come si risolvono le disequazioni logaritmiche in cui al secondo membro c’è una costante, cioè un numero diverso da 0.![]()
Abbiamo già visto che la disequazione, considerando anche la condizione di esistenza può essere riscritta aggiungendo f(x)>0.
La “b” della disequazione con il logaritmo può essere riscritta come “1·b”. Ricordandoci la regola dei logaritmi per cui un logaritmo con base e argomento uguali fa sempre 1, allora possiamo riscrivere.
- a>1 : quando la base del logaritmo è maggiore di 1 non cambia nulla ai segni o ai versi della disequazione.
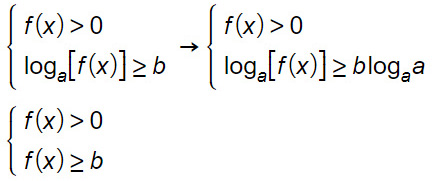
- 0<a<1 : quando la base del logaritmo è compresa tra 0 e 1, il maggiore (o maggiore e uguale) diventa minore (o minore e uguale) e viceversa.
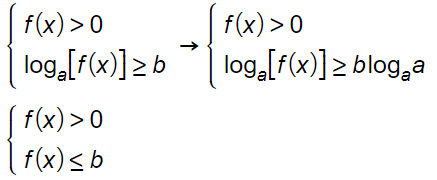
Disequazione logaritmica di tipo 3
L’ultimo caso è quello più ricorrente. Vengono considerate dagli studenti le disequazioni logaritmiche più difficili: stiamo parlando di quelle in cui sono presenti più di un logaritmo. Vediamo come risolverle.
Se le basi dei logaritmi sono uguali diventa tutto più semplice. Si risolve semplicemente considerando gli argomenti dei logaritmi, come abbiamo già fatto nelle disequazioni di tipo 2. In parole povere basta eliminare il logaritmo.
Se invece dobbiamo risolvere disequazioni logaritmiche con basi diverse, allora dobbiamo usare la formula vista per il cambiamento di base:
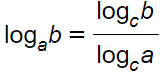
Per cui possiamo riscrivere il nostro caso come:
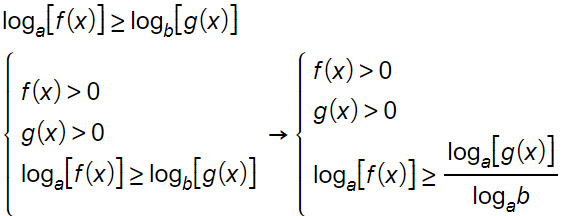
Vedrai negli esercizi che il denominatore è un numero, per cui puoi scriverlo come una frazione. Considerando anche la base del logaritmo, anche in questo caso abbiamo due possibilità:
- se a>1 : argomento del logaritmo maggiore di 1
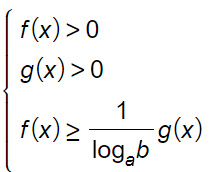
- se 0<a<1 : argomento del logaritmo compreso tra 0 e 1, si modifica il verso della disequazione.
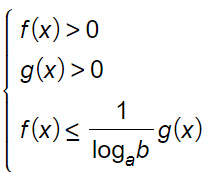
Un consiglio per imparare a risolvere le disequazioni logaritmiche
Sconsigliamo sempre ai nostri studenti di imparare a memoria le formule viste fino a questo momento. E’ più importante invece capire come risolvere disequazioni logaritmiche di qualsiasi tipo con un unico metodo universale.
Ecco come procedere:
- si trasforma la disequazione logaritmica in un sistema in cui alle prime righe metteremo le condizioni di esistenza. All’ultimo rigo riscriviamo invece la disequazione con i logaritmi.
- risolviamo le tre disequazioni, trasformando l’ultima e facendo in modo di avere ai due membri due logaritmi con la stessa base.
- si valuta la base del logaritmo. Se maggiore di 1 non si modifica nulla e si risolve. Se la base è compresa tra 0 e 1 allora si inverte il segno.
- alla fine si mettono a sistema graficamente le disequazioni per trovare la soluzione finale.
Disequazioni logaritmiche esercizi svolti
Esercizio 1
Risolvere la seguente disequazione logaritmica
log(x-1)>1
Svolgimento
Affinché la disequazione abbia senso è necessario imporre subito le condizioni di esistenza. Queste possono essere scritte subito oppure essere messe a sistema con la disequazione con il logaritmo.
x-1>0
x>1
Procediamo a questo punto trasformando l’1 al secondo membro. Ricordati che quando la base del logaritmo è sottintesa vuol dire che è pari a “e” (Numero di Nepero)
log(x-1)>loge
x-1>e
x>e+1
Da notare che, essendo la base e maggiore di 1, non sono stati modificati i versi della disequazione. Riportiamo il tutto su un unico grafico:
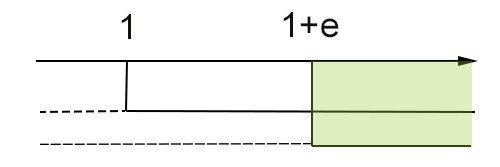
Il risultato finale è:
x>1+e
Esercizio 2
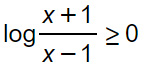
Rientriamo ora nel caso delle disequazioni logaritmiche fratte. Il procedimento non cambia. Ovviamente dovremo risolvere delle disequazioni fratte che sono un po’ più impegnative delle normali disequazioni.
Iniziamo risolvendo la condizione di esistenza del logaritmo:
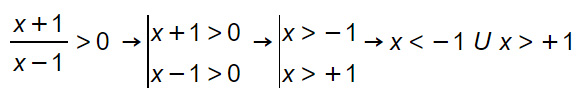
Passiamo ora alla disequazione con il logaritmo:
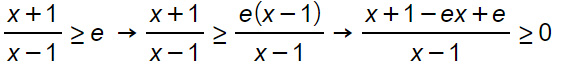
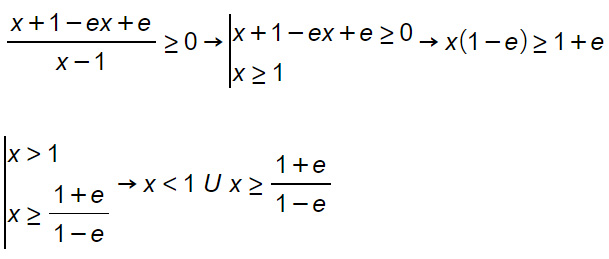
A questo punto mettiamo a sistema le due soluzioni delle disequazioni su un unico grafico.
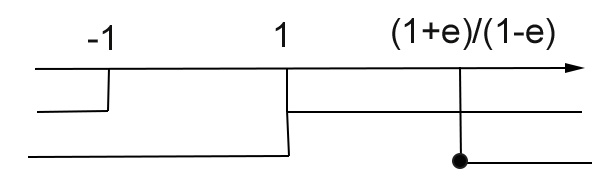
x<1 U x≥(1+e)/(1-e)