L’applicazione delle regole dei radicali all’interno delle equazioni o delle disequazioni mette spesso in difficoltà gli studenti. Per questa ragione, abbiamo deciso di realizzare questa piccola guida ai tanti che ci hanno chiesto un supporto e un po’ di disequazioni coi radicali già svolte.
Per poter risolvere questo tipo di esercizi, è necessario saper risolvere le disequazioni di primo grado e le fratte. Se hai già letto queste lezioni, allora sei pronto per rendere il livello dell’esercizio un po’ più complesso e risolvere con noi le disequazioni a coefficienti irrazionali.
Disequazioni con coefficienti irrazionali
Attento a non far confusione!
Prima di partire con l’esercitazione, è doveroso fare una premessa: non confondere le disequazioni coi radicali con le disequazioni irrazionali. Negli esercizi di oggi vedremo delle espressioni in cui nella radice sono presenti esclusivamente dei numeri, mentre nelle disequazioni irrazionali è anche l’incognita x ad essere sotto la radice.
Esercitazione svolta
Esercizio 1)
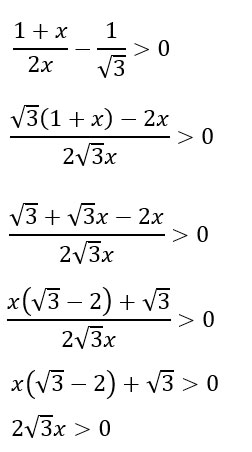
A questo punto, dopo aver diviso numeratore e denominatore della disequazione a coefficienti irrazionali, andiamo ad eseguire la razionalizzazione sul numeratore.
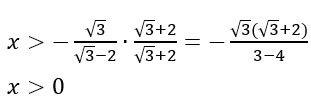
Cambiamo della prima disequazione coi radicali ottenuta sia il segno che il verso così che il -1 al denominatore diventi +1
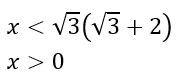
A questo punto possiamo sistemare i nostri risultati sul grafico e prendere le soluzioni con il segno positivo (perché la disequazione di partenza N/D>0 aveva il verso maggiore)
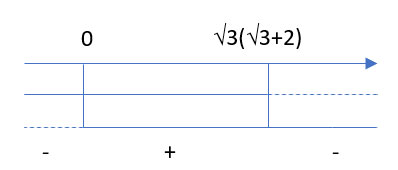
Dovendo prendere quindi valori positivi, il risultato dell’esercizio sarà quello interno.
Esercizio 2)
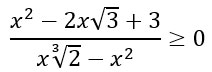
Il primo passaggio è come sempre quello di “spezzare” numeratore e denominatore così da risolvere quello che viene chiamato falso sistema. Poiché nella traccia compare il verso maggiore e uguale , è importante NON riportare l’uguale al denominatore (sarebbe errore grave, poiché il denominatore non può essere mai uguale a zero).
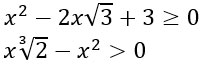
A questo punto possiamo risolvere entrambe le disequazioni con coefficienti irrazionali. La prima possiamo risolverla scomponendola con la regola del quadrato di binomio, mentre per la seconda basta raccogliere l’incognita x.
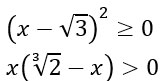
Anche la seconda disequazione posso spezzarla in due, considerando entrambi i fattori maggiori di zero. La prima, essendo un quadrato, è sempre positiva con l’aggiunta del valore che rende la funzione nulla, cioè x uguale a radice di 3.
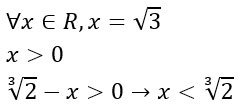
A questo punto possiamo inserire i risultati ottenuti sul grafico.
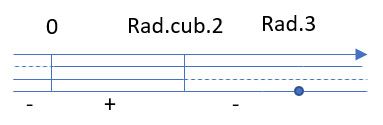
Ecco quindi che il risultato finale sarà:
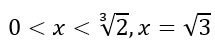
Esercizio 3
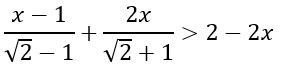
Si parte con il calcolo del minimo comune multiplo al denominatore.
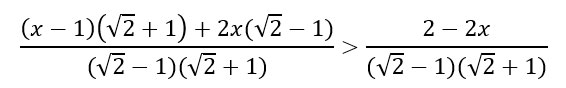
Al secondo membro non abbiamo riportato il prodotto delle due parentesi con la radice perché il loro prodotto è pari a 1. Prova a calcolare infatti radical 2 meno 1 che moltiplica radical 2 più 1 con la regola della somma per differenza che abbiamo studiato nei prodotti notevoli.
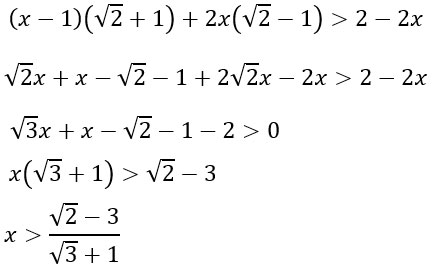
Conclusioni
Abbiamo visto che nelle disequazioni a coefficienti irrazionali è importante seguire le regole generali viste per svolgere le normali disequazioni. Il consiglio che possiamo darti è di trattare le radici come se fossero un oggetto separato dai numeri e dall’incognita x e seguire le regole sui radicali applicando quando necessario le razionalizzazioni.
Se questa lezione ti è stata utile, ti chiediamo di lasciare un commento. Ci aiuterà a crescere e a migliorare la qualità delle lezioni che mettiamo a disposizione a te e agli studenti di tutta Italia.