La discontinuità di terza specie, detta anche eliminabile, si ha quando esistono, sono finiti ed uguali il limite destro e sinistro rispetto al punto c. Tuttavia i limiti non coincidono con il valore della funzione nel punto c, cioè con f(c).
Tradotto in linguaggio matematico, la discontinuità di terza specie si può scrivere come:
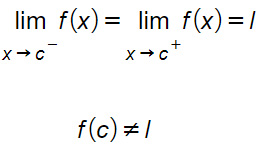
Dalla formula si nota come il limite sinistro e destro della funzione f(x) nel punto c siano finiti e pari al valore l. Tuttavia i limiti non sono uguali al valore che la funzione assume nel punto c, cioè f(c). In questo caso non c’è un salto così come avveniva negli altri tipi di discontinuità.
Esempio 1
Vediamo in un esercizio svolto in cui abbiamo una funzione con una discontinuità di terzo tipo
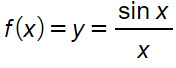
Se proviamo a calcolare il dominio della funzione, essendoci il denominatore lo imponiamo diverso da zero. Per cui il dominio è:
Dominio: x≠0
Calcoliamo ora il limite destro e sinistro della funzione. Ci possiamo rendere conto che si tratta di un limite notevole il cui risultato è unico. Per cui limite destro e sinistro coincidono e sono pari a:
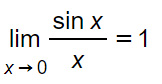
Quindi abbiamo una situazione in cui f(0) non esiste, mentre i limiti sono finiti, uguali e pari a 1. E’ quindi una discontinuità di terza specie.
Osservazione
Su alcuni libri di testo ci viene fatto notare come questo tipo di discontinuità può essere eliminata andando a “ridefinire” la funzione f(x) nel punto singolare attribuendole il valore l del limite. Nell’esempio possiamo prolungare f(x) con continuità in x=0 e possiamo considerare la nuova funzione:
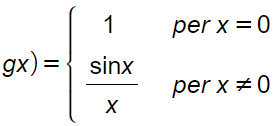
Abbiamo definito continua una funzione y=f(x) che, in un punto c del suo dominio, soddisfi la condizione.
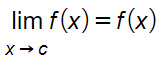
Nel nostro esempio questa condizione è verificata, per cui nonostante la discontinuità di terza specie, la funzione è continua in x=0.
Esercizio svolto
Studiamo i punti di discontinuità della seguente funzione reale:
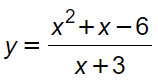
Iniziamo calcolando il dominio, imponendo il denominatore diverso da zero.
Dominio: x+3≠0 → x≠-3
Calcoliamo ora il limite della funzione per x che tende a -3.
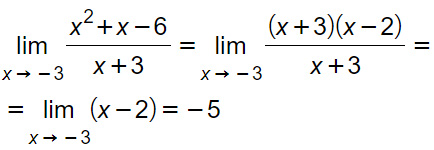
Come è stato risolto? Al numeratore abbiamo un polinomio di secondo grado che abbiamo scomposto usando le regole delle scomposizioni così da semplificare con il denominatore. Alla fine abbiamo il limite pari a -5.
Quindi la funzione f(x) presenta una discontinuità di terza specie per x=-3.
Spiegazione esauriente e semplice . Soddisfatta. Grazie