Come si calcola la direttrice della parabola? Quali sono le formule da utilizzare? In questa lezione vedremo in maniera più approfondita qual è l’equazione della direttrice di una parabola attraverso anche l’aiuto di alcuni esercizi svolti e commentati.
Ti ricordi la definizione di parabola? Abbiamo visto che è il luogo geometrico dei punti del piano equidistanti da un punto fisso F detto fuoco e da una retta detta direttrice.
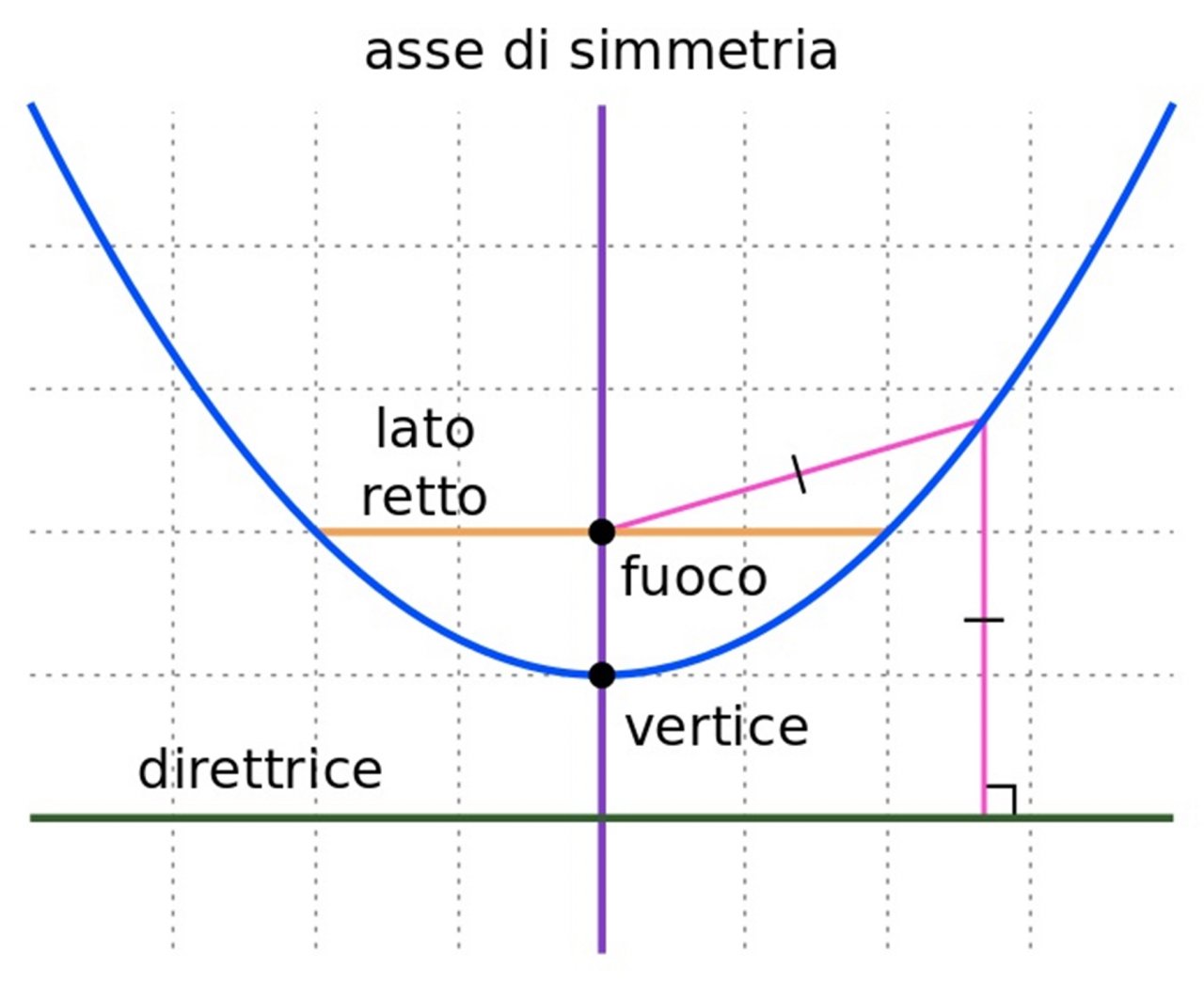
La direttrice della parabola è segnata in verde
Direttrice parabola – definizione
La direttrice di una parabola è una retta la cui distanza da un punto generico P della parabola è uguale alla distanza P dal fuoco F.
L’equazione della direttrice è generalmente molto semplice e si scrive come l’equazione di una retta.
CARATTERISTICHE
Come è possibile notare anche dal grafico in alto, la retta è orizzontale nel caso in cui la parabola ha asse di simmetria verticale.
Viceversa, quando l’asse di simmetria è orizzontale, la direttrice della parabola è una retta verticale.
Formula direttrice parabola ad asse verticale
Ci troviamo in questo caso di fronte ad una parabola di equazione:
![]()
In tal caso l’equazione della direttrice della parabola è:
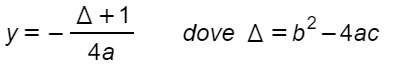
Ti ricordi di Δ (delta)? E’ il discriminante che si utilizza anche nelle equazioni di secondo grado nel metodo del delta.
Formula direttrice parabola ad asse orizzontale
L’equazione in questo caso è:
![]()
La direttrice della parabola in questo caso è una retta verticale di equazione:
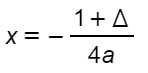
Direttrice parabola: esercizi svolti
Esercizio 1
Determinare la direttrice della parabola di equazione:
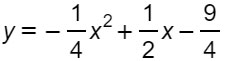
Svolgimento
Semplicemente va applicata l’equazione vista sopra per parabola ad asse verticale. Per cui possiamo scrivere:
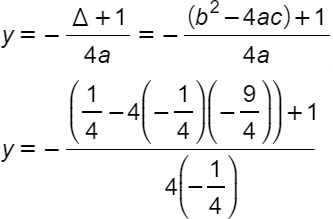
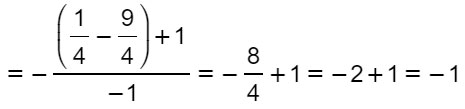
L’equazione della direttrice della parabola è quindi: y=1
Esercizio 2
Una parabola ha vertice nell’origine degli assi cartesiani, asse coincidente con l’asse delle ordinate e direttrice di equazione y=4/3. Scrivi l’equazione della parabola.
Svolgimento
Questo secondo esercizio è leggermente più complesso del precedente. Abbiamo le coordinate del vertice della parabola V(0;0), l’asse di simmetria x=0 e la direttrice.
Scriviamo i dati a disposizione:
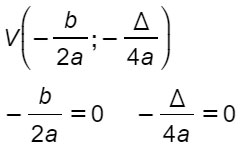
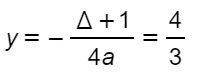
Possiamo scrivere i dati in colonna, così da ottenere un sistema di equazioni con le tre incognite a, b e c.
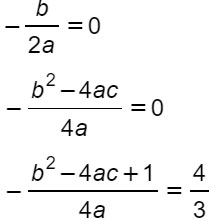
Dalla prima equazione otteniamo immediatamente che b=0. Per cui sostituendo nelle altre due, il risultato è:
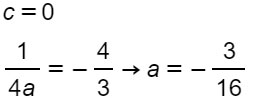
Abbiamo così terminato l’esercizio e ricavato le tre incognite. Il risultato è corretto anche perché, essendo una parabola con vertice nell’origine, ci ritroviamo i due coefficienti b=c=0.
Se vuoi continuare ad esercitarti, vai agli esercizi sulla parabola.