Nelle precedenti lezioni ci siamo occupati delle proprietà dei logaritmi, andando ad analizzare come si sviluppano le operazioni matematiche principali. In questa lezione andiamo ad approfondire la regola della differenza di logaritmi.
Inizieremo facendo un piccolo riepilogo sulla formula da utilizzare e poi vedremo qualche esercizio, così da capire anche quali sono i possibili casi da risolvere.
Formula della differenza di logaritmi
La sottrazione tra due logaritmi è un nuovo logaritmo con la stessa base e il rapporto degli argomenti.
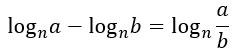
Ovviamente vale anche la relazione inversa. Ovvero avendo un logaritmo con una frazione, questa può essere trasformata in una differenza di logaritmi.
Fin qui tutto facile, no? La sottrazione diventa una divisione e viceversa. Il problema, come vedremo negli esercizi, c’è quando bisogna risolvere la differenza di logaritmi con una base differente. Procediamo però con ordine e soprattutto in maniera semplice.
Differenza di logaritmi con la stessa base
E’ il caso più semplice, in cui sono legati dal segno “meno” due logaritmi che hanno la stessa base. E’ sufficiente applicare alla lettera la formula che abbiamo appena visto. Facciamo subito un esempio.
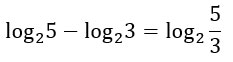
Come puoi vedere esercizi simili si risolvono in unico passaggio! Che ci sia un’incognita x o un radicale, la regola non cambia.
Differenza di logaritmi con base diversa
In questo caso non ci troviamo nella situazione di poter applicare la formula vista in alto. Occorre prima fare in modo che i due logaritmi abbiano la stessa base, cioè bisogna applicare la regola del cambiamento di base dei logaritmi. Vediamo con un esempio come si procede:
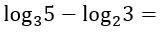
Ci sono due possibilità: o il logaritmo in base 3 lo si trasforma in base 2, oppure il secondo logaritmo in base 2 lo si trasforma in base 3. Puoi decidere tu quale strada percorrere, non cambia nulla!
Proviamo a cambiare il secondo logaritmo:
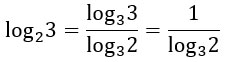
Cosa abbiamo fatto? Il logaritmo di partenza diventa una frazione dove:
- al numeratore ho un logaritmo con nuova base e argomento precedente
- al denominatore ho un logaritmo con nuova base e come argomento la vecchia base.
Riscriviamo quindi il nostro esercizio:
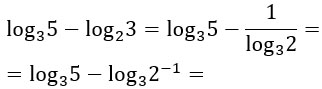
Che cosa è stato fatto? Ti ricordi la regola delle potenze negative? L’esponente negativo lo si trasforma in positivo e si invertono numeratore e denominatore. A questo punto utilizziamo la regola delle potenze di logaritmi, per cui l’esponente diventa un coefficiente – cioè si porta fuori dal logaritmo.
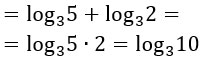
Conclusione
Come hai potuto notare la differenza di logaritmi può essere risolta in due modi a seconda che la base sia la stessa o meno. Nel primo caso è sufficiente applicare la formula vista ad inizio lezione.
Nel caso in cui, invece, le due basi siano differenti, sarà necessario operare un piccolo cambiamento di base così da ricondurci al caso precedente.
Forse ti interessa anche: somma di logaritmi – formula ed esempi svolti