La differenza di cubi è un tipo di scomposizione appartenente alla famiglia dei prodotti notevoli. Grazie a questa semplice regola è possibile scomporre la differenza tra due cubi nel prodotto di un binomio di primo grado per un trinomio di secondo grado.
In questa lezione vedremo come si scompone la differenza di due cubi del tipo:
x³-a³
E’ una regola molto utilizzata durante le espressioni e gli esercizi e, per quanto possa sembrare difficile, in realtà vedremo che è molto facile imparare a memoria come si scompone la differenza di cubi. Come sempre, nella seconda parte di questa lezione vedremo alcuni esempi ed esercizi svolti per mettere subito in pratica la formula.
Scomposizione con differenza di cubi
Come già detto sopra, consideriamo la differenza di due cubi generici x³-a³. Per fare la scomposizione la formula da seguire è la seguente:
![]()
La differenza di cubi è pari al prodotto di un binomio di primo grado per un trinomio di secondo grado. Il nostro consiglio è di impararla a memoria imparando la logica che c’è dietro piuttosto che provare a ricavarla ogni volta.
Come ricordarla – il trucco per gli studenti
Qual è la regola che c’è dietro questa formula? Prova ad osservare il secondo membro. Abbiamo il prodotto tra due polinomi. Il primo è un binomio identico al primo membro ma senza gli esponenti. Il secondo invece è un trinomio molto simile ad un quadrato di binomio ma non c’è il 2 con il doppio prodotto e i segni sono tutti positivi.
Proviamo a mettere in pratica questa regola facendo un esempio:
x³-8 → Poiché 8 è pari a 2³, allora possiamo vedere la traccia come x³-2³. Applichiamo a questo punto la formula vista:
x³-a³=(x-a)(x²+ax+a²) dove ovviamente a=2
x³-2³ = (x-2)(x²+2x+4).
Attenzione a non confondere la differenza di cubi con il cubo di un binomio o con la differenza di quadrati. In questo caso abbiamo delle potenze con indice dispari.
Dimostrazione della differenza di cubi
Ti stai chiedendo come si arriva ad ottenere la formula che abbiamo visto? Semplicemente proviamo a risolvere il prodotto che compare al secondo membro dell’equazione:
(x-a)(x²+ax+a²) =
= x³+ax²+a²x–ax²-a²x-a³ =
Eliminiamo tutti i termini opposti e alla fine otteniamo:
= x³-a³.
Differenza di binomi ad indice dispari
Anche se l’esponente non è 3, è possibile fare la scomposizione di polinomi: la cosa importante è che l’indice della potenza sia dispari. Vediamo subito le formule per scomporre un binomio:
![]()
Possiamo quindi sintetizzare la regola per la differenza di cubi e più in generale per la scomposizione di binomi di grado dispari come:
La differenza di potenze con identico esponente dispari si scompone nel prodotto della differenza delle basi per un polinomio di 1 grado inferiore, ordinandolo così che abbia le potenze decrescenti del primo monomio e crescenti del secondo, i segni sono tutti positivi.
Esempi ed esercizi svolti
Eseguire le scomposizioni delle seguenti differenze di cubi.
Esercizio 1
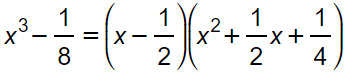
In questo primo esercizio c’è una differenza di due cubi con le frazioni. Non lasciarti spaventare e applica la formula vista considerando a=1/2.
Esercizio 2
x³-1=(x-1)(x²+x+1)
In questo caso non ci sono particolari difficoltà a risolvere l’esercizio. Basta applicare la formula.
Esercizio 3
![]()
In questo caso la differenza di cubi inizia a diventare un po’ più complessa. Infatti il 2 che trovi come primo coefficiente non ha una radice cubica naturale, per cui quando andremo ad eseguire la scomposizione dovremo ricordarci di applicare la radice cubica.
Esercizi da risolvere
Gli esercizi che ti proponiamo di risolvere non hanno riportato la soluzione intenzionalmente. Sono elencati non solo delle sottrazioni di cubi, ma anche le somme di cubi (trovi la lezione a questo link). Sono molto semplici per cui mettiti alla prova come se stessi affrontando un compito in classe.
Scomporre in fattori le seguenti somme e differenze di cubi.

Per domande o chiarimenti, o se la lezione è stata di tuo aiuto, lascia un commento. Il nostro staff ti risponderà nel minor tempo possibile.