Elia ci pone la domanda: qual è la derivata del seno di x e come si può dimostrare? Come ci si comporta per risolvere la derivata di seno di f(x), cioè in cui nell’argomento della funzione goniometrica sin c’è una funzione? E’ possibile avere qualche esercizio svolto?
RISPOSTA
La derivata di senx fa parte di quelle che vengono definite derivate fondamentali e si risolve in un solo passaggio:
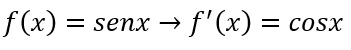
La regola è estremamente semplice: la derivata del seno di x è uguale al coseno di x. Per poterla dimostrare, ricorriamo al calcolo del limite del rapporto incrementale, così come ci insegna la definizione di derivata.
Derivata seno – dimostrazione
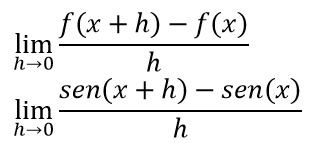
Al posto di f(x) abbiamo messo senx e al posto di f(x+h) abbiamo messo il seno di (x+h). A questo punto applichiamo le formula di addizione per il seno:
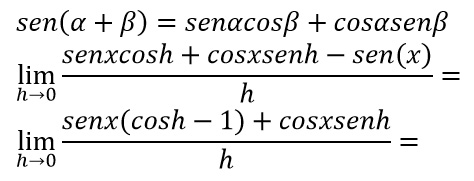
Possiamo a questo punto dividere il limite in due ed ottenere:
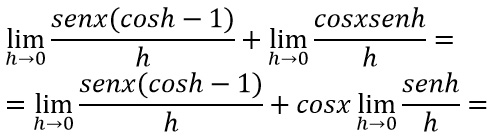
Guarda ora il secondo elemento di questa somma. C’è il limite per h che tende a 0, di senh fratto h: lo hai riconosciuto? E’ il limite notevole del seno e il risultato è proprio 1.
Aggiungiamo inoltre una specie di razionalizzazione dei radicali. Moltiplico e divido per la stessa quantità al numeratore ma con il segno opposto. In questo modo ottengo il prodotto di una somma per una differenza.
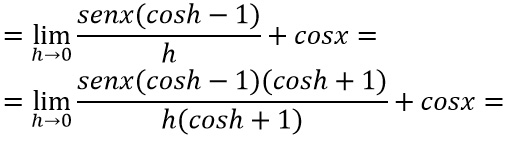
A questo punto svolgiamo la moltiplicazione al numeratore:
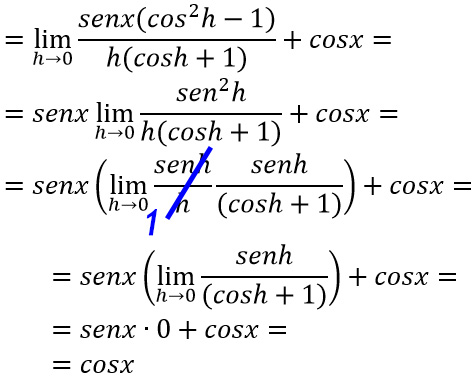
Abbiamo così dimostrato il valore della derivata del seno di x. Su altri appunti o libri di testo troverai che per la dimostrazione possono essere utilizzate anche le formule di prostaferesi: è assolutamente indifferente. Scegli il metodo che preferisci.
A questo punto iniziamo a complicare un pochino il calcolo della derivata ed introduciamo la funzione composta.
Derivata seno f(x)
Come si calcola la derivata di sen f(x), cioè nel caso in cui c’è una funzione come argomento del seno? La regola è identica al caso precedente: la derivata del seno di f(x) è uguale al coseno di f(x) per la derivata della funzione, cioè f'(x). Quindi la formula da seguire è:
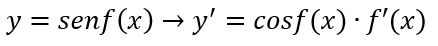
Proviamo a vedere assieme qualche esempio così da mettere in pratica proprio quest’ultima formula, che sarà quella che più utilizzerai negli esercizi o nei compiti.
Derivata del seno esercizi svolti
ESERCIZIO 1
Calcolare la derivata seno 2x. Come procedere? Essendo una funzione composta, distinguiamo le operazioni che vengono eseguite sulla x in ordine:
- la x viene moltiplicata per 2
- il risultato diventa argomento del seno
Visto che le derivate delle funzioni composte si risolvono partendo dall’ultima operazione, iniziamo proprio dal seno:
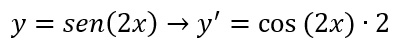
Come abbiamo risolto? Si calcola la derivata del seno di f(x), che è quindi cos f(x), ovvero il coseno di 2x. Si moltiplica infine per la derivata di f(x), ovvero per la derivata di 2x, cioè 2.
ESERCIZIO 2
Proviamo a calcolare ora derivata seno al quadrato. Anche in questo caso si tratta di una funzione composta. Vediamo alla x quali operazioni sono applicate in successione:
- la x è argomento del seno
- il risultato va elevato al quadrato
Utilizziamo quindi per prima la derivata del quadrato e poi moltiplichiamo per la derivata del seno.
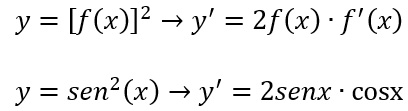
Puoi notare che il risultato finale (2senxcosx) può essere espresso anche come sen2x utilizzano le formule di duplicazione.
ESERCIZIO 3
Il risultato sarebbe molto diverso se la traccia ti chiedesse di determinare la derivata del seno di x al quadrato. In tal caso la prima operazione applicata alla x è il quadrato, mentre la seconda è il seno. Per cui in tal caso si usa la formula y=senf(x) che derivato diventa y’=[cosf(x)]*f'(x). Prova da solo a risolvere e confrontare il risultato con l’esercizio 2.
Approfondimenti: calcolo derivata arcoseno
Se questa lezione ti è stata utile, continua a seguirci e lasciaci un feedback nei commenti. Ci aiuterai a rispondere alle tante domande che ci arrivano ogni giorno da voi studenti. Buono studio!