In questa breve lezione vedremo in maniera davvero semplice come si calcola la derivata di una radice. Analizzeremo un piccolo trucchetto che ti eviterà di imparare nuove formule e con cui potrai effettuare rapidamente il calcolo della derivata prima della radice.
Calcolare la derivata di una radice – non serve una formula!
In molti libri di testo, nel formulario delle derivate fondamentali, viene espressa una formula per poter calcolare la derivata di una radice – quadrata, cubica, … Noi ti consigliamo invece un metodo molto più veloce e che utilizza le proprietà delle potenze e le proprietà dei radicali.
Ti ricordi come si fa a trasformare una radice in una potenza (e viceversa)?
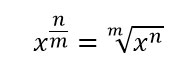
E’ sufficiente ricordare che quando hai una potenza con una frazione, il numeratore resta l’esponente, mentre il denominatore sta ad indicare l’indice di radice. Come ha a che fare questa regola con le derivate con radici?
E’ davvero semplicissimo: trasformiamo la radice in una potenza e poi calcoliamo la derivata prima della potenza. Proviamo a fare qualche esempio.
Derivata di una radice esercizi svolti
Derivata di radice di x
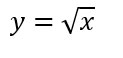
Come calcolare la derivata della radice quadrata di x? Eseguiamo subito la trasformazione da radice in potenza. In questo caso non c’è un esponente per cui è sottinteso 1, mentre l’indice della radice è 2, visto che si tratta di una radice quadrata.
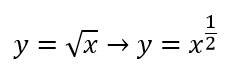
A questo punto possiamo risolvere l’esercizio calcolando la derivata della potenza x elevato a 1/2.
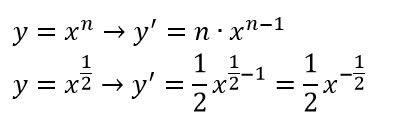
A questo punto potremmo considerare l’esercizio già finito, ma è preferibile esprimere la nuova potenza in una maniera matematicamente più elegante. Per farlo ricordiamoci quello che avevamo studiato nella lezione sulle potenze negative: quando c’è un segno meno all’esponente ciò che è al numeratore passa al denominatore e viceversa. Anche l’esponente 1/2 può essere trasformato nuovamente in radice.
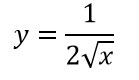
Derivata di una radice cubica
Con il metodo che abbiamo visto possiamo eseguire la derivata prima di qualsiasi tipo di radice, indipendentemente da quale sia l’indice del radicale. Non ci credi? Proviamo a svolgere la derivata della radice cubica di x.
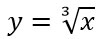
Come nell’esercizio precedente, trasformiamo la radice in potenza e poi ne calcoliamo la derivata:
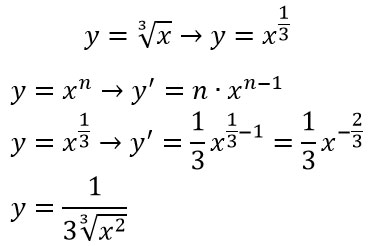
Visto quanto è stato semplice? Se invece vuoi proprio una formula risolutiva da inserire nel tuo formulario, possiamo ricavarla assieme seguendo questo stesso metodo e utilizzando l’indice di radice generico n.
Derivata di una radice generica
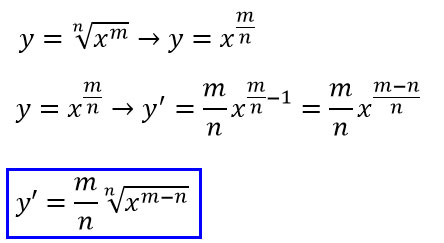
Quindi la derivata prima della radice generica con esponente m e indice di radice n è pari al rapporto m/n per la radice ennesima di x elevato a m-n.
Derivata radice composta
Come si calcolano le derivate delle radici nel caso in cui abbiamo non più x sotto radice ma una funzione f(x)? Si applicano semplicemente le regole viste nella lezione sulle derivate composte. Quindi si risolve la derivata della radice di f(x) come fatto fino ad ora e poi alla fine si moltiplica semplicemente per la derivata dell funzione f(x).
Vediamo subito un esempio pratico: calcoliamo la derivata della radice cubica del logaritmo di x.
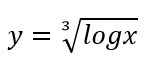
Trasformiamo la radice in potenza e seguiamo il procedimento visto fino ad ora. Alla fine dovremo semplicemente aggiungere il prodotto per la derivata del logaritmo, cioè 1/x.
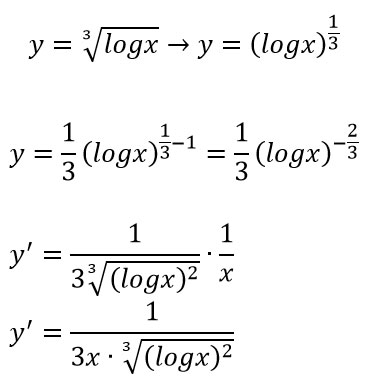
Ovviamente l’esercizio sarebbe molto differente se si dovesse calcolare la derivata del logaritmo della radice di x:
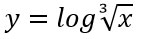
In questo caso si parte con la derivata del logaritmo per primo e poi si moltiplica per la derivata della radice quadrata di x. Lasciamo a te la risoluzione di questo piccolo ma interessante esercizio. Ovviamente se hai problemi o hai bisogno di qualche altro suggerimento, lasciaci un commento sotto.
Se la lezione è stata dai tuo interesse, lasciaci un tuo feedback positivo: ogni commento positivo è per noi uno stimolo per proseguire con la realizzazione e la pubblicazione di lezioni gratuite per gli studenti di tutta Italia e di tutte le età.