Andrea ci scrive: “Quanto vale la derivata dell’arcotangente? Come si calcola e come possiamo ricavare e dimostrarne il risultato applicando la definizione di derivata di arctg di x?”
RISPOSTA
La derivata della funzione arcotangente fa parte di quelle che si chiamano derivate fondamentali, una tabella che abbiamo visto nelle precedenti lezioni in cui sono presenti le derivate prime di tutte le funzioni: dalla derivata di una costante sino a quella della funzione arcoseno. In questa tabella si legge che derivata arctg x si può calcolare come:
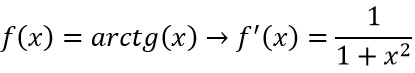
Dimostrazione derivata arcotangente
Generalmente questa operazione non viene dimostrata con il metodo del rapporto incrementale, ma si utilizza la regola di derivazione sulle funzioni inverse. Partiamo però con calma e facciamo un passo alla volta così vedrai che diventa tutto più semplice.
L’arcotangente è la funzione inversa della funzione tangente. Cioè se f(x)=tg(x), allora possiamo scrivere:
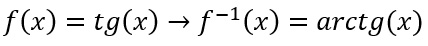
PICCOLA PREMESSA: Sappiamo che la funzione arcotangente è continua in tutto R, visto la sua curva non ha interruzioni su tutto l’asse delle x, è invertibile e la sua funzione inversa, come detto, è proprio la tangente. Tutto ciò considerando un intervallo compreso tra -π/2 e + π/2 (meno pi-greco mezzi e più pi-greco mezzi): questo perché in questo intervallo anche la funzione tangente risulta continua.
Usiamo quindi la regola che vale per la derivata delle funzioni inverse. Se non la ricordi, non preoccuparti. Eccola:
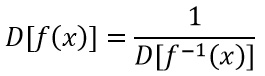
Quindi adattando la formula al nostro caso, possiamo scrivere che la derivata dell’arcotangente è uguale a 1 fratto la derivata della tangente. Ricordiamo che quest’ultima è pari a 1 fratto il coseno al quadrato di x.
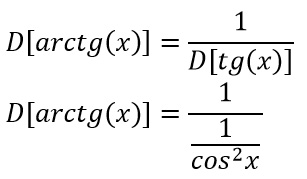
A questo punto pensiamo a come trasformare l’1 presente al denominatore. Ricordi le relazioni fondamentali della goniometria? La più importante – e che ti consigliamo di ricordare perché ti sarà sempre molto utile – è che la somma dei quadrati del seno e del coseno è pari a 1.
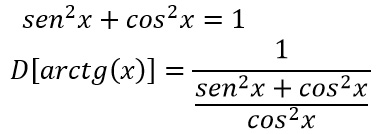
Spezziamo quindi la frazione presente al denominatore in due addendi:
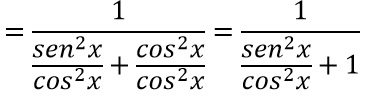
A questo punto, sapendo che la tangente di un angolo è il rapporto tra seno e coseno, possiamo semplificare l’espressione matematica ottenuta e riscrivere:
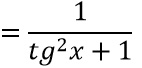
Visto che abbiamo fatto la derivata della funzione inversa, la nostra x in realtà è l’arcotangente e quindi possiamo sostituire:
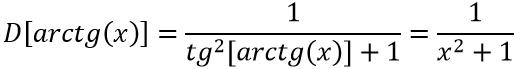
Abbiamo così ottenuto e dimostrato il risultato che cercavamo.
Derivata arcotangente di f(x)
Ne parleremo in maniera più dettagliata nella lezione sulle derivate delle funzioni composte, ma cosa succede quando dobbiamo calcolare la derivata dell’arcotangente di una funzione? La regola è sempre la stessa, ma ricordati di aggiungere al risultato finale un prodotto con la derivata della funzione argomento dell’arcotangente. Cioè vale:
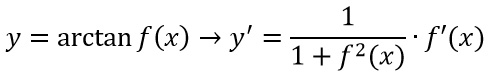
Esercizio svolto
Proviamo a vedere un esempio assieme. Prova a calcolare la derivata della seguente funzione.
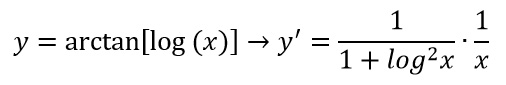
Come puoi vedere in questo caso l’argomento dell’arcotangente è la funzione logaritmo. Questo vuol dire che seguiamo la formula della derivata dell’arcotangente ma al denominatore al posto della x ci sarà il log(x). Inoltre si aggiunge un segno “per” con la derivata del logaritmo, cioè 1 su x.
Conclusioni
Se questa lezione ti è stata d’aiuto, lasciaci un feedback positivo nei commenti. Ogni tua considerazione ci aiuterà a migliorare la qualità delle nostre lezioni e a rispondere alle tante domande di voi studenti. Buono studio 😉