Uno dei concetti più importanti nella geometria elementare riguarda la definizione di angolo. In questa pagina vedrai che cos’è un angolo. Partendo dalla definizione che trovi sui libri di matematica, cercheremo di fare qualche esempio facile anche attraverso l’uso di immagini ed esempi.
Definizione angolo
Si chiama angolo ciascuna delle due parti in cui un piano rimane diviso da due semirette r ed s aventi la stessa origine O.
Spiegazione
Quella che hai visto enunciata è la definizione di angolo presente in tutti i libri di matematica e geometria. Ma che cosa vuol dire? Innanzitutto è importante che tu ricordi la definizione di semiretta.
A questo punto immagina che il tuo foglio da disegno sia un piano, quindi uno spazio bidimensionale, su cui possiamo andare a disegnare due semirette consecutive, cioè con un estremo in comune.

Come puoi vedere tra le due semirette disegnate si generano due angoli, α e β, che in figura trovi indicati con due colori differenti.

E’ importante sottolineare che mentre le rette e le semirette si indicano con l’alfabeto latino in lettera minuscola, gli angoli si indicano con le lettere minuscole dell’alfabeto greco. Quando invece l’angolo si forma grazie a due segmenti consecutivi, può essere indicato usando gli estremi dei segmenti stessi. Ecco l’esempio in figura.
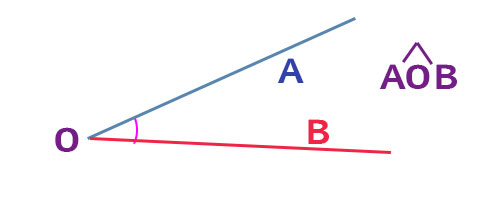
Nell’immagine puoi vedere come i segmenti AO e OB abbiamo l’estremo O in comune. Tra loro si formano due angoli: quello interno che abbiamo indicato e quello esterno (non presente in figura). In entrambi i casi l’angolo lo definiamo AOB con quel cappelletto sulla lettera dell’angolo, che va messa sempre al centro.
Proprietà e definizioni di angoli
Le due semirette r ed s si dicono lati dei due angoli alfa e beta ottenuti nell’immagine precedente. L’origine O delle due semirette si chiama vertice di ciascuno dei due angoli. I punti di un angolo non appartenenti ai suoi lati si dicono punti interni all’angolo. I punti di un angolo non appartenenti ai suoi lati si dicono ad esso esterni. Si chiama infine contorno di un angolo l’insieme formato dai suoi due lati.
Si ammette inoltre che un angolo contiene tutti i punti di ogni semiretta OP che ha l’origine nel vertice O dell’angolo e passa per un punto P interno all’angolo; una così fatta retta si dice interna all’angolo.
Definizione di angolo – conclusioni
A parte gli enunciati finali che ti abbiamo presentato e che non userai moltissimo, le definizioni di angoli sono piuttosto semplici e non richiedono particolari sforzi di memoria. Per questa ragione ti consigliamo di rileggere la lezione se qualcosa non ti è chiaro, o di contattarci se hai dubbi o perplessità.