La cotangente di un angolo in trigonometria viene definita come il rapporto tra coseno e seno. Può anche essere definita come l’inverso della tangente.
In questa lezione vedremo nel dettaglio che cos’è e qual è il grafico della cotangente, analizzandone l’andamento nel piano cartesiano, le definizioni e i valori noti da ricordare (o come ricavarli).
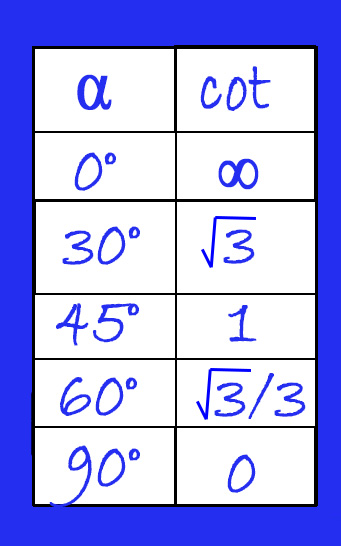
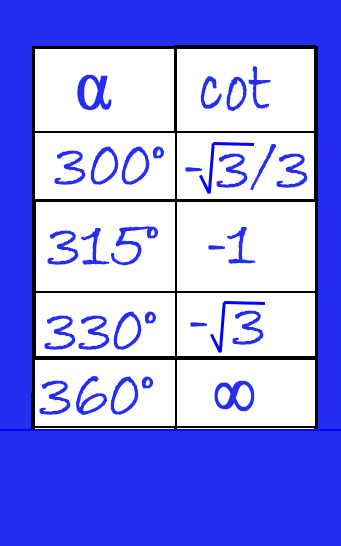
Valori cotangente – la tabella riassuntiva


Definizione di cotangente
Consideriamo la circonferenza goniometrica e l’arco AB con A(1;0) e B(xB,yB). Detto C il punto di coordinate cartesiane (0;1), mandiamo la retta tangente alla circonferenza t per il punto A e la tangente s per il punto C come nel grafico seguente.
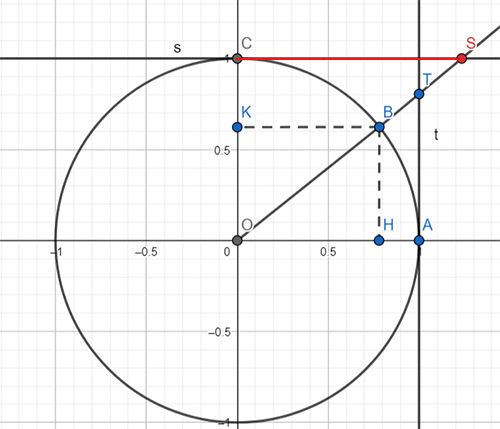
Se la retta s interseca la retta OB in un punto S, diremo che l’ascissa di S è la cotangente dell’angolo AOB. Si può quindi scrivere dal punto di vista matematico:
cotg AOB = xs
La cotangente di un angolo si indica con cotg oppure con ctg.
Poiché ys=1 perché coincide con il raggio della circonferenza goniometrica (che è unitario), allora possiamo anche scrivere:
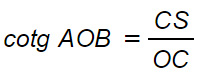
Per la similitudine dei triangoli OAT e OHB, considerando che H e K sono le proiezioni di B sull’asse delle ascisse e delle ordinate, allora si ha:
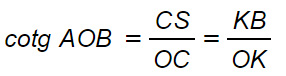
dove KB e OK sono rispettivamente il coseno e il seno dell’angolo.
La cotangente si definisce quindi come il rapporto tra coseno fratto seno dell’angolo.
Caratteristiche della cotangente
Come per il seno e il coseno, si può dimostrare che la cotangente di un angolo non dipende dall’unità di misura scelta, ossia dal raggio della circonferenza goniometrica, ma dipendono esclusivamente dall’ampiezza dell’arco.
Ai fini pratici c’è da ricordare che la cotangente non ha un’unità di misura, cioè è un numero adimensionale. Non dovrai quindi aggiungere cm, dm, m, o gradi dopo l’indicazione del valore.
Il segno della funzione cotangente
La cotangente dell’angolo è positiva se B appartiene al primo o al terzo quadrante, ossia per 0°<α<90° oppure 180°<α<270°.
Assume invece un valore negativo se B appartiene al secondo o al quarto quadrante, ossia se 90°<α<180° oppure 270°<α<360°.
Grafico cotangente
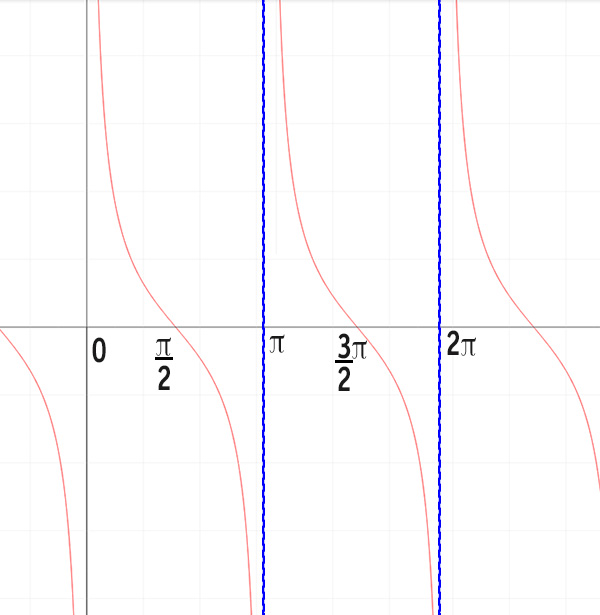
Per costruire il grafico della cotangente è sufficiente ricordarsi i valori degli angoli noti per il seno e il coseno. In particolare:
- quando α=0 → cosα=1 senα=0 → cotgα=cosα/senα=∞
- quando α=90° (π/2) → cosα=0 senα=1 → cotgα=cosα/senα=0
- quando α=180° (π) → cosα=-1 senα=0 → cotgα=cosα/senα=∞
- quando α=270° (2/3 π/) → cosα=0 senα=-1 → cotgα=cosα/senα=0
- quando α=360° (2π) → cosα=1 senα=0 → cotgα=cosα/senα=∞
Da quello che si nota nel grafico della cotangente, se l’angolo AOB è uguale a 0° o a 180°, la retta OB del primo disegno di questa lezione è parallela alla retta s, per cui in tali casi non esiste la cotangente.
Dominio cotangente – discontinuità e asintoti
La funzione cotangente è di tipo periodico e, proprio come la tangente, si ripete in maniera ciclica ogni 180°. Per questa ragione, quando si risolve un esercizio si esplicita sempre alla fine la periodicità aggiungendo un …+kπ.
Come puoi vedere dal grafico, la cotangente non è una funzione continua perché ha diversi punti di discontinuità e si generano degli asintoti verticali in tutto il grafico.
Volendo calcolare il dominio della funzione cotangente, possiamo scrivere che:
D: ∀x∈R-{x=kπ}
Questo vuol dire che la funzione è sempre continua tranne per α=0° con tutti i valori della periodicità: 0+kπ =kπ. Questo vuole dire che ci sono degli asintoti verticali in corrispondenza di 0, 180°, 360°, 540°, …
Esempi sulla cotangente
Dato l’angolo 90°<α<180°, determiniamo le condizioni che deve soddisfare il parametro m affinché sia verificata la seguente uguaglianza.
(m+2)cotgα=-3m
Svolgimento
Attraverso un semplice passaggio algebrico trasformiamo l’equazione.
cotgα=-3m/(m+2)
Visto che l’angolo si trova nel II quadrante, la cotangente ha un valore negativo. Per questa ragione deve essere soddisfatta la condizione:
-3m/(m+2)<0
Si tratta di una normale disequazione fratta di primo grado con l’incognita m. Risolvendo otteniamo infatti:
3m/(m+2)>0
m>0
m+2>0
m<-2 U m>0