Il coseno iperbolico si indica con il simbolo matematica cosh(x) ed appartiene alle funzioni iperboliche, una famiglia di funzioni con caratteristiche simili a quelle goniometriche. Mentre però queste ultime si basavano sulla circonferenza goniometrica, seno e coseno iperbolico si definiscono a partire dall’iperbole equilatera.
Definizione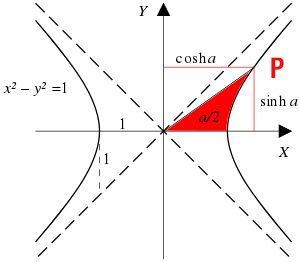
Si disegni sul piano cartesiano un’iperbole equilatera centrata nell’origine del sistema di riferimento. Essa avrà equazione X²-Y²=1. Dato il generico angolo α, è possibile individuare il settore iperbolico (disegnato in rosso in figura) di angolo α/2. Uno dei vertici di questa figura è il punto P.
Il coseno iperbolico è l’ascissa del punto P
cosh(x)=xP
Come tutte le altre funzioni iperboliche, cosh(x) si può definire attraverso le funzioni esponenziali. In particolare si può scrivere che:
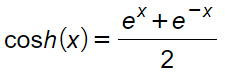
Il coseno iperbolico è dato dalla media di ex e e-x.
Proprietà
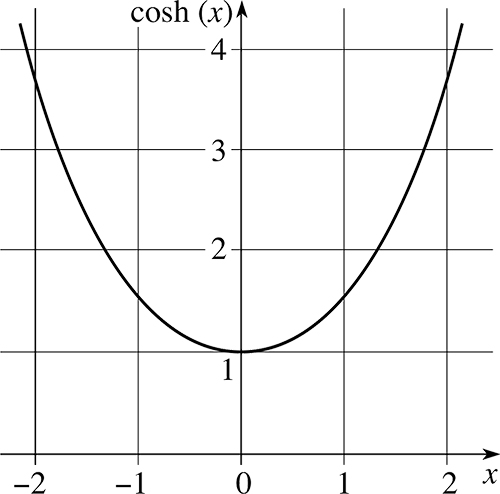
Grafico del coseno iperbolico
Al grafico disegnato sul piano cartesiano si arriva facilmente attraverso un normale studio di funzione che ti riportiamo di seguito.
Dominio
Per analizzare il campo di esistenza di questa funzione, partiamo dalla sua definizione in termini esponenziali. Il dominio del coseno iperbolico è dato dall’unione di quello di ex e e-x. Poiché entrambi sono continui su tutto R (vedi dominio della funzione esponenziale), allora vale che:
D: ∀ x∈R
o anche
D=(-∞;+∞)
Il cosseno iperbolico è una funzione continua in tutto R.
Simmetrie
Poiché vale la relazione f(x)=f(-x), cioè
ex + e-x = e(-x) + e-(-x)
allora la funzione è pari. Questo vuol dire che il coseno iperbolico è simmetrico rispetto all’asse delle ordinate.
Intersezioni con gli assi
Per calcolare gli zeri della funzione, si impone x=0.
y=(ex + e-x)/2
y=(e0 + e-0 )/2 → y=1
Abbiamo quindi scoperto un’interessante analogia con il coseno. Cioè per x=0, y=1
cosh(0)=1
Studio del segno, positività
Come si fa normalmente nello studio di funzione, si impone y>0, cioè:
y=(ex + e-x)/2>0
Poiché sia ex che e-x sono entrambi positivi, allora anche la loro somma sarà positiva. Questo vuol dire che il coseno iperbolico è una funzione sempre positiva, cioè sul grafico si trova sempre al di sopra dell’asse delle ascisse.
Limiti agli estremi
Sia il limite per x che tende a meno infinito che per x che tende a più infinito, portano come risultato a più infinito.
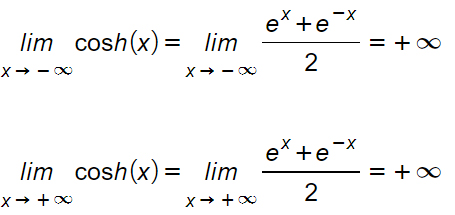
Derivata ed integrale
Riprendendo l’analogia con il coseno, la derivata del coseno iperbolico è pari al seno iperbolico cambiato di segno.
d(coshx)=-sinhx
Allo stesso modo, l’integrale sarà uguale al seno iperbolico a meno di una costante k.
∫cosh(x)dx=sinh(x)+k