Il codominio di una funzione matematica è il sottoinsieme in cui sono contenute le immagini della funzione.
Dominio e codominio sono senza dubbio uno degli argomenti più importanti ma allo stesso tempo più difficili per gli studenti delle superiori. In tanti ci hanno chiesto che cos’è e come trovare il codominio di una funzione.
In questa lezione vedremo di spiegare, attraverso anche degli esempi pratici, che cos’è il codominio, come si definisce e come si calcola in maniera semplice senza rischio di fare errori.
Definizione codominio
Ti ricordi la definizione di funzione matematica? Avevamo detto che è una relazione tra due insiemi A e B per cui, per ogni elemento di A, si associa uno e un solo elemento di B.
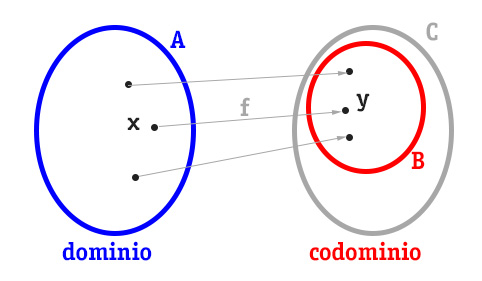
L’insieme di partenza A è detto dominio della funzione, mentre il sottoinsieme B, formato dalle immagini di A, si definisce codominio della funzione f.
Attenzione: non confondere le immagini della funzione con il codominio. Mentre infatti le immagini sono gli elementi che da A sono passati in B, il codominio di una funzione è l’insieme che contiene le immagini.
Quindi diremo che gli elementi x appartengono al dominio, mentre gli elementi y appartengono al codominio.
Codominio esercizi ed esempi
Di seguito vediamo due esercizi svolti che ci aiuteranno a capire come si trova il codominio di una funzione.
Il primo esempio è un po’ più semplice, generalmente viene assegnato come esercitazione quando si studiano dominio e codominio. Il secondo esercizio è invece più complesso e potrebbe essere la traccia di un compito in classe.
Esercizio 1
Determinare il codominio delle seguenti funzioni, di cui è dato il dominio A.
![]()
Svolgimento
La traccia ci fornisce alcuni elementi del dominio. La prima cosa da fare è quindi determinare le immagini degli elementi di A, come nel grafico sotto…
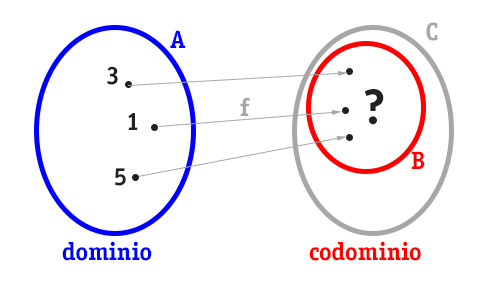
Calcoliamo quindi f nei 3 punti datici dalla traccia. Praticamente andiamo a sostituire ciascuno dei tre punti al posto della x della funzione.
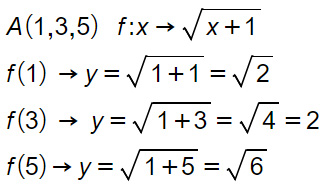
Il codominio della funzione è l’insieme che chiamiamo C costituito dai 3 elementi trovati. Per cui se il dominio è D{1,3,5), il codominio è:
![]()
Ricordati che il codominio di una funzione è un insieme e come tale va espresso attraverso delle parentesi graffe.
Esercizio 2
Studiare dominio e codominio della funzione:
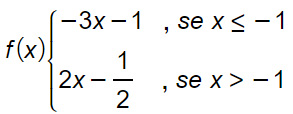
Svolgimento
Uno dei modi più semplici per trovare il codominio di una funzione è l’analisi del suo grafico. Se ricordiamo l’equazione della retta, possiamo renderci subito conto che la funzione è formata da 2 rette: la prima arriva fino a x minore è uguale di 1. Subito dopo vale la seconda retta.
Per cui possiamo disegnare il grafico:
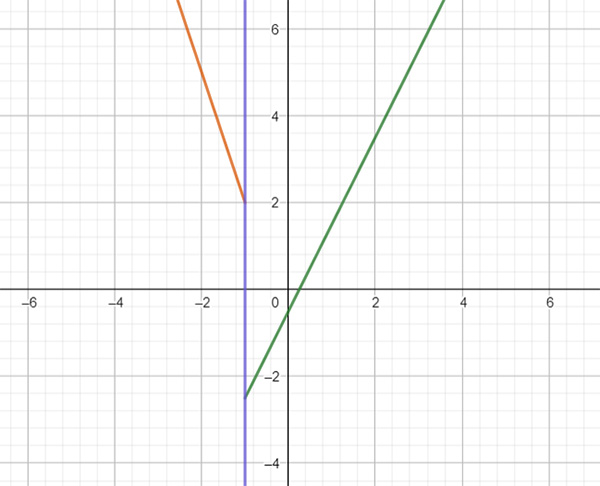
La retta arancione è -3x-1, mentre quella in verde è 2x-1/2. Si può notare che non si tratta di una funzione continua, poiché nel punto di ascissa x=1 c’è una discontinuità di prima specie, cioè c’è un salto.
Il dominio è: D(-∞;-1] U [+1;+∞)
Per calcolare il codominio si uniscono i codomini delle due funzioni. Per quanto riguarda la prima funzione, quella arancione, si parte dal valore +2 e si va a +∞.
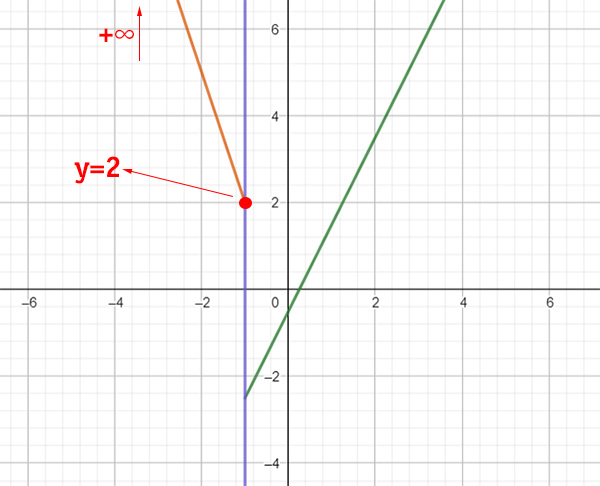
Per quanto riguarda la retta y=2x-1/2, vediamo dal grafico sotto che parte dal punto -5/2 (che si può calcolare sostituendo il valore -1 al posto della x) e va a infinito.
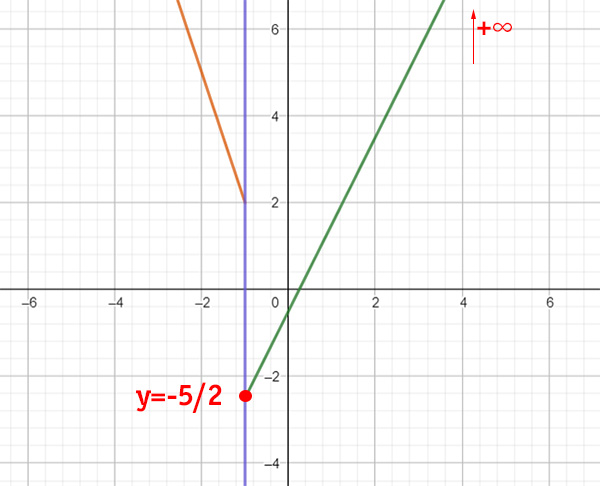
Unendo i due grafici possiamo dire che, partendo dal basso:
- si parte da y=-5/2
- c’è un’interruzione per y=-2
- si tende poi a + infinito.
Il risultato finale, cioè il codominio della funzione è:
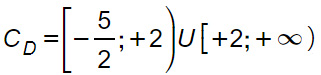
Esercizio 3
Trovare il codominio di una funzione esponenziale
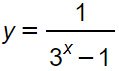
Svolgimento
Per trovare il codominio di una funzione possiamo applicare un altro metodo oltre a quello grafico visto nell’esercizio 2.
Che cos’è il codominio? Alcuni lo definiscono come il dominio della funzione di arrivo. Per cui basta calcolare la funzione inversa e trovarne il dominio. Ecco come procedere:
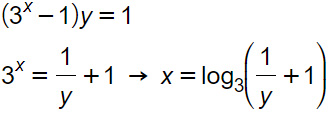
Per trovare il codominio a questo punto imponiamo l’argomento del logaritmo strettamente maggiore di 0.
Bisognerà a questo punto risolvere una semplice disequazione fratta di primo grado per ottenere la soluzione.
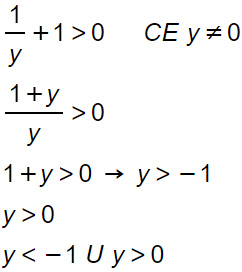
Possiamo quindi scrivere in maniera “più elegante” come:
![]()
Conclusioni
In questa lezione abbiamo visto come si calcola il codominio di una funzione matematica utilizzando ben 3 diversi metodi di calcolo.
L’ultimo, in realtà, è il più utilizzato perché permette di trovare la soluzione anche quando le funzioni da analizzare sono più complesse.
Se questa lezione è stata di tuo aiuto e se ci sono ancora dei dubbi sull’argomento, lascia un commento in basso. Il nostro staff ti risponderà nel minor tempo possibile.